Признак Лейбница — различия между версиями
| Строка 1: | Строка 1: | ||
'''Признак Лейбница''' - это признак сходимости для определения сходимости '''знакопеременного [[ряд]]а''' [[файл:РЯД001.png]]. | '''Признак Лейбница''' - это признак сходимости для определения сходимости '''знакопеременного [[ряд]]а''' [[файл:РЯД001.png]]. | ||
== Условие применимости == | == Условие применимости == | ||
| − | Признак Лейбница применим для знакопеременного ряда [[файл: | + | Признак Лейбница применим для знакопеременного ряда [[файл:РЯД001.png]] при условиях [[файл:РЯД037.png]]. |
== Формулировка == | == Формулировка == | ||
Если для знакопеременного ряда [[файл:РЯД001.png]] выполняются условия [[файл:РЯД037.png]], т.е. начиная с некоторого номера, для всех '''n''' выполняется условие монотонности убывания до нуля, то ряд [[файл:РЯД001.png]] – сходится. | Если для знакопеременного ряда [[файл:РЯД001.png]] выполняются условия [[файл:РЯД037.png]], т.е. начиная с некоторого номера, для всех '''n''' выполняется условие монотонности убывания до нуля, то ряд [[файл:РЯД001.png]] – сходится. | ||
Версия 12:54, 23 марта 2023
Признак Лейбница - это признак сходимости для определения сходимости знакопеременного ряда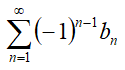 
.
Условие применимости
Признак Лейбница применим для знакопеременного ряда 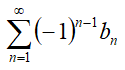при условиях 
.
Формулировка
Если для знакопеременного ряда 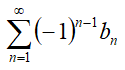выполняются условия , т.е. начиная с некоторого номера, для всех n выполняется условие монотонности убывания до нуля, то ряд 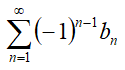– сходится.
Другие признаки:
Ссылки
- Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. М.: «Наука», 1975.
- Участник:Logic-samara
