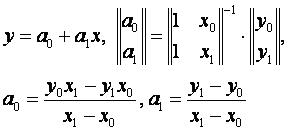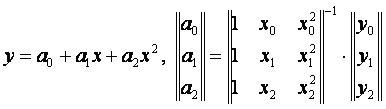Интерполяция каноническим многочленом — различия между версиями
(начало) |
|||
| Строка 22: | Строка 22: | ||
*Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970. | *Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
| − | [[Категория:Численные методы]] | + | [[Категория:Математика]][[Категория:Численные методы]] |
Текущая версия на 15:30, 6 апреля 2023
Интерполяция каноническим многочленом - это определение коэффициентов многочлена n-ой степени, проходящего через заданные (n+1)-у точку. Значения в точке определяются по формуле многочлена.
Содержание
Формула
Заметим что канонический многочлен это многочлен n-ой степени, как и формула Лагранжа. В случае когда необходимо многократное вычисление многочлена n-ой степени в различных точках, предпочтительнее использование формулы канонического многочлена.
Линейная интерполяция
При n=1 канонический многочлен имеет вид:
Квадратическая интерполяция
При n=2 канонический многочлен имеет вид:
Кубическая интерполяция
При n=3 канонический многочлен имеет вид:
Другие формулы:
- Линейная интерполяция;
- Интерполяция каноническим многочленом;
- Интерполяционная формула Бесселя;
- Интерполяционная формула Бесселя на середину;
- Интерполяционная формула Гаусса вперёд (первая формула);
- Интерполяционная формула Гаусса назад (вторая формула);
- Интерполяционная формула Лагранжа;
- Интерполяционная формула Ньютона вперёд (первая формула);
- Интерполяционная формула Ньютона назад (вторая формула);
- Интерполяционная формула Стирлинга.
Ссылки
- Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970.
- Участник:Logic-samara
