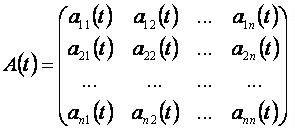Матричная система дифференциальных уравнений динамического процесса — различия между версиями
(начало) |
(нет различий)
|
Текущая версия на 06:19, 8 февраля 2021
Матричная система дифференциальных уравнений динамического процесса — это система дифференциальных уравнений, описывающая процесс во времени, в которой дифференциальные уравнения являются элементами матрицы.
Содержание
Обозначения
Введём обозначения


Матричная система дифференциальных уравнений имеет вид:
Полагая матрицу коэффициентов A постоянной, получаем матричную систему линейных дифференциальных уравнений.
Пример 1
Матрица 
Матрица 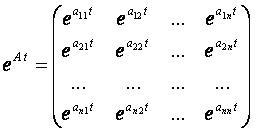
Пример 2
Матрица 
Другие системы:
Ссылки
- Р. Беллман. Введение в теорию матриц. М.: Наука, 1976, стр.191.
- Участник:Logic-samara