Одноканальная СМО без очереди и с ограниченным временем обслуживания

Одноканальная СМО без очереди и с ограниченным временем обслуживания

Одноканальная СМО без очереди и с ограниченным временем обслуживания — это система массового обслуживания, в которой есть каналы обслуживания, но нет очереди: если заявка приходит, в момент, когда все каналы свободны, то она немедленно обслуживается любым одним каналом, если заявка приходит - когда уже обслуживаются заявки числом меньше, чем число каналов, то она немедленно обслуживается одним из свободных каналов, иначе если заявка приходит - когда заняты все каналы, то заявка покидает систему (теряется). При обслуживании заявки проявляют «нетерпение». Максимальное число заявок в системе равно числу каналов.

Обозначения

n – число каналов обслуживания, ;

m – число мест в очереди;

λ – интенсивность простейшего потока заявок;

μ – интенсивность простейшего потока обслуживания;

η – интенсивность простейшего потока уходов заявки с обслуживания.

Описание модели

На вход одноканальной СМО поступает простейший поток заявок с интенсивностью λ.

Интенсивность простейшего потока обслуживания каждого канала μ.

Если заявка застаёт все каналы свободными, она принимается на обслуживание и обслуживается любым одним из n-каналов. При этом заявка проявляет «нетерпение».

Если заявка застаёт свободным хотя бы один канал, то она принимается на обслуживание любым из свободных каналов и обслуживается, проявляя «нетерпение».

Если заявка застаёт все каналы занятыми, то она получает отказ (покидает систему не обслуженной).

После окончания обслуживания одной заявки освобождается один канал.

Состояние рассмотренной системы будем связывать с числом заявок, находящихся в системе.

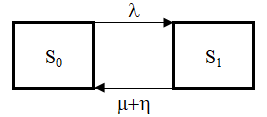
Граф состояний

М/М/1/0 – Одноканальная СМО без очереди и с ограниченным временем обслуживания.

Рассмотрим множество состояний системы:

S₀ – в системе нет ни одной заявки, все каналы свободны;

S₁ – в системе имеется 1-заявка, она обслуживается 1-каналом.

Система дифференциальных уравнений

Система дифференциальных уравнений, описывающих поведение системы, имеет вид:

Рассмотрим стационарный режим работы системы (при t→∞).

Система линейных уравнений

Система уравнений принимает вид:

Решение системы линейных уравнений

Решим систему относительно p₀,p₁.

В результате получаем решение системы: Файл:СЛУ1t02.png

Другие СМО:

1. СМО n-канальная без очереди;
2. СМО n-канальная без очереди и с ограниченным временем обслуживания;
3. СМО n-канальная без очереди и со случайным результатом обслуживания;
4. СМО n-канальная без очереди и со случайным выбором канала;
5. СМО n-канальная без очереди и с взаимопомощью;
6. СМО n-канальная без очереди и с частичной взаимопомощью;
7. СМО n-канальная с m-очередью;
8. СМО n-канальная с m-очередью и с ограниченным временем обслуживания;
9. СМО n-канальная с m-очередью и со случайным результатом обслуживания;
10. СМО n-канальная с m-очередью и с ограниченным временем ожидания;
11. СМО n-канальная с m-очередью и с ограниченным временем обслуживания и ожидания;
12. СМО n-канальная с m-очередью и с взаимопомощью;
13. СМО n-канальная с m-очередью и с частичной взаимопомощью;
14. СМО n-канальная с бесконечной очередью;
15. СМО с бесконечным числом каналов;
16. СМО замкнутая n-канальная без очереди;
17. СМО замкнутая n-канальная без очереди и с взаимопомощью;
18. СМО замкнутая n-канальная без очереди и с частичной взаимопомощью;
19. СМО замкнутая n-канальная без очереди и с k-источниками;
20. СМО замкнутая n-канальная без очереди, с k-источниками и с взаимопомощью;
21. СМО замкнутая n-канальная без очереди, с k-источниками и с частичной взаимопомощью;
22. СМО замкнутая n-канальная с m-очередью;
23. СМО замкнутая n-канальная с m-очередью и с взаимопомощью;
24. СМО замкнутая n-канальная с m-очередью и с частичной взаимопомощью;
25. СМО замкнутая n-канальная с m-очередью и с k-источниками;
26. СМО замкнутая n-канальная с m-очередью, с k-источниками и с взаимопомощью;
27. СМО замкнутая n-канальная с m-очередью, с k-источниками и с частичной взаимопомощью.