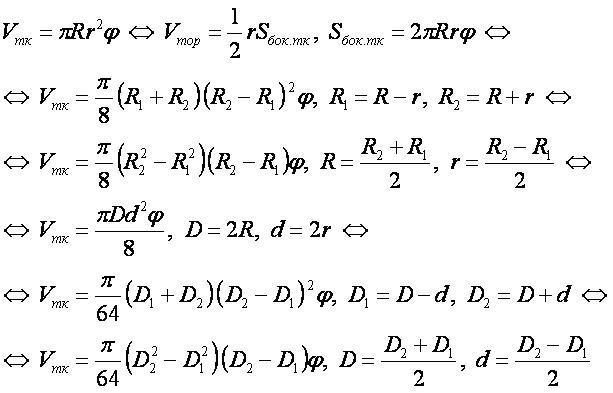Объём торового клина — различия между версиями
м |
м |
||
| Строка 32: | Строка 32: | ||
[[файл:ОТК01.JPG]] | [[файл:ОТК01.JPG]] | ||
*Заметим, что при '''φ=π/2''' объём '''торового клина''' совпадает с четвертью объёма '''[[Объём тора|тора]]'''. | *Заметим, что при '''φ=π/2''' объём '''торового клина''' совпадает с четвертью объёма '''[[Объём тора|тора]]'''. | ||
| − | == [[ | + | == [[Объём трёхмерной фигуры|Другие фигуры:]] == |
{{Список ОФВ}} | {{Список ОФВ}} | ||
== Ссылки == | == Ссылки == | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Версия 05:31, 11 февраля 2021
Объём торового клина — это объём, пропорциональный величине центрального двугранного угла, части объёма тора.
Под торовым клином будем подразумевать наименьшую часть тора, вырезаемую центральным двугранным углом из тора. Торовый клин является изогнутым цилиндром.
Содержание
Обозначения
Введём обозначения:
R — радиус окружности вращения образующей окружности тора;
r — радиус образующей окружности тора;
R2 — внешний радиус тора;
R1 — внутренний радиус тора;
D — диаметр окружности вращения образующей окружности тора;
d — диаметр образующей окружности тора;
D2 — внешний диаметр тора;
D1 — внутренний диаметр тора;
φ — центральный двугранный угол;
Sбок.тк — площадь боковой поверхности;
Sосн.тк — площадь одного основания;
Vтк — объём торового клина, ограниченный тором и двугранным углом.
Формула
- Заметим, что при φ=π/2 объём торового клина совпадает с четвертью объёма тора.
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- параболоидное копыто;
- шаровая бочка;
- круговая бочка;
- параболическая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.