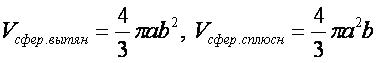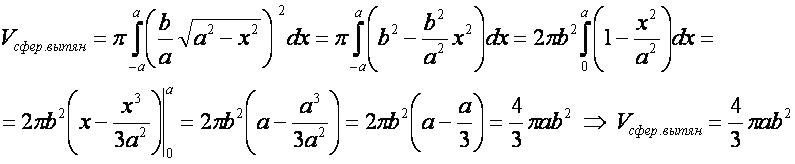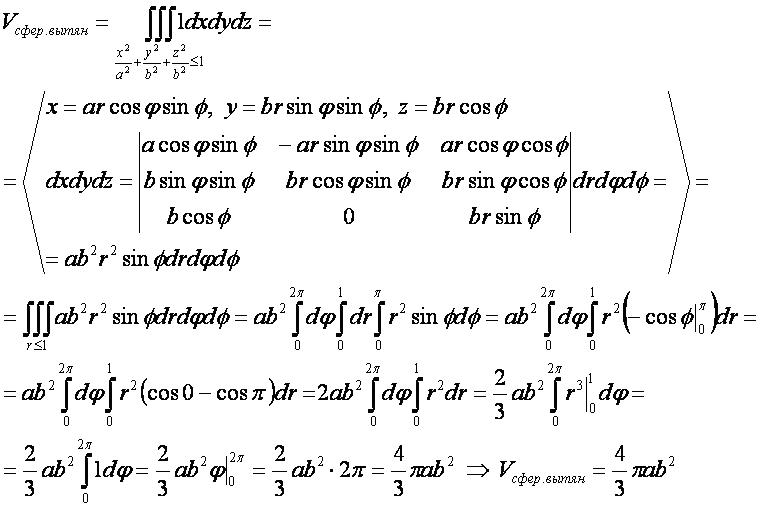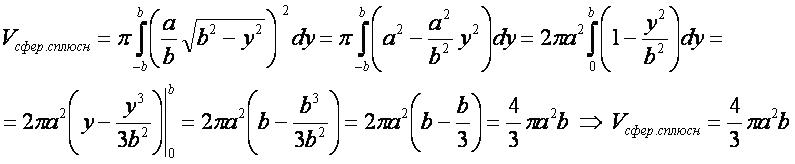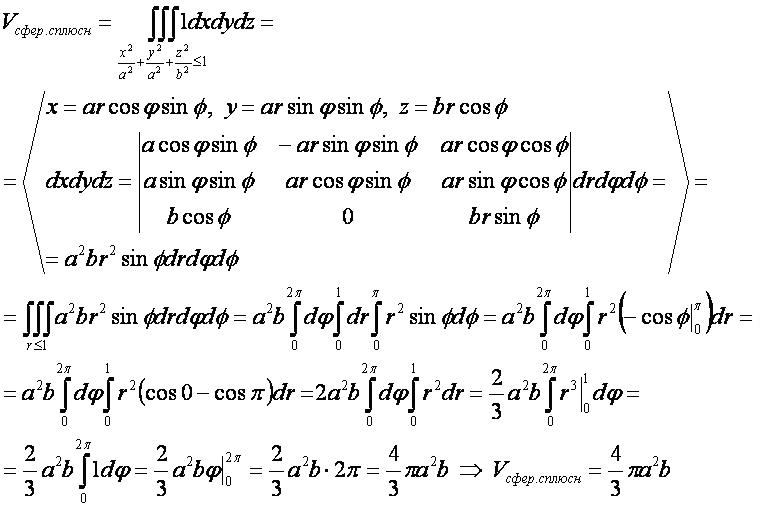Объём сфероида — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 51: | Строка 51: | ||
*Для вывода используется формула '''"[[объём трёхмерной фигуры]]"''' в прямоугольных координатах. | *Для вывода используется формула '''"[[объём трёхмерной фигуры]]"''' в прямоугольных координатах. | ||
*Для нахождения интеграла используется '''[[метод замены переменных]]''' и переход к сферическим координатам. | *Для нахождения интеграла используется '''[[метод замены переменных]]''' и переход к сферическим координатам. | ||
| − | == Другие фигуры: == | + | == [[Объём трёхмерной фигуры|Другие фигуры:]] == |
{{Список ОФВ}} | {{Список ОФВ}} | ||
== Ссылки == | == Ссылки == | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 05:35, 11 февраля 2021
Объём сфероида — это число, характеризующее сфероид в единицах измерения объёма.
Сфероид — это тело, ограниченное эллипсоидом вращения.
Эллипсоид вращения — это поверхность в трёхмерном пространстве, образованная вращением эллипса вокруг одной из его осей.
Содержание
Виды сфероидов:
- вытянутый;
- сплюснутый;
- нормальный.
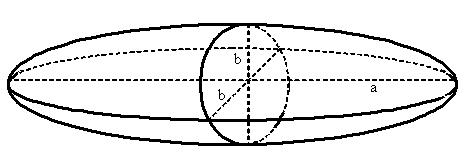
Вытянутый сфероид ограничен вытянутым эллипсоидом вращения.
Вытянутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до двух заданных точек (фокусов) постоянна (равна большой оси). Вытянутый эллипсоид вращения получается вращением эллипса вокруг большой оси. У вытянутого эллипсоида вращения одна большая ось и две малые оси.
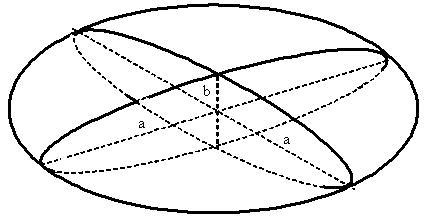
Сплюснутый сфероид ограничен сплюснутым эллипсоидом вращения.
Сплюснутый эллипсоид вращения — это геометрическое место точек пространства, для которых сумма расстояний до ближайшей и до наиболее удалённой точки заданной окружности постоянна (равна малой оси). Сплюснутый эллипсоид вращения получается вращением эллипса вокруг малой оси. У сплюснутого эллипсоида вращения две большие оси и одна малая ось.
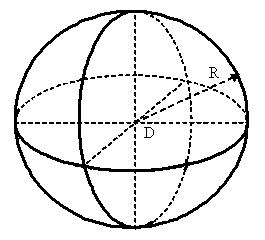
Нормальный сфероид — это шар (ограничен сферой).
Обозначения
Введём обозначения:
a — большая полуось;
b — малая полуось;
Vсфер.вытян — объём вытянутого сфероида.
Vсфер.сплюсн — объём сплюснутого сфероида.
Формулы:
- Заметим, что при a=b формула объёма сфероида превращается в формулу объёма шара.
Вывод формул:
Объём вытянутого сфероида
1-ый способ
- Для вывода используется формула 1 "объём фигуры вращения".
2-ой способ
- Для вывода используется формула "объём трёхмерной фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется метод замены переменных и переход к сферическим координатам.
Объём сплюснутого сфероида
1-ый способ
- Для вывода используется формула 2 "объём фигуры вращения".
2-ой способ
- Для вывода используется формула "объём трёхмерной фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется метод замены переменных и переход к сферическим координатам.
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- параболоидное копыто;
- шаровая бочка;
- круговая бочка;
- параболическая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.