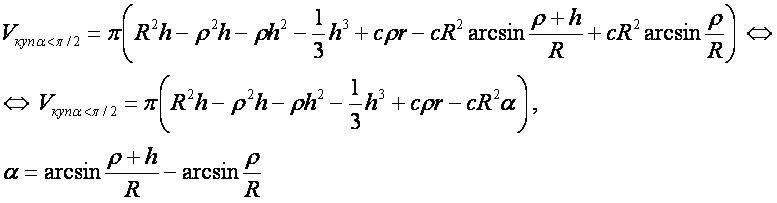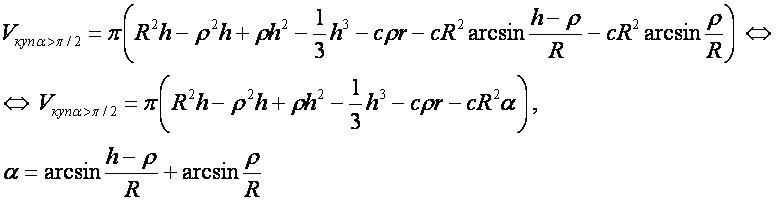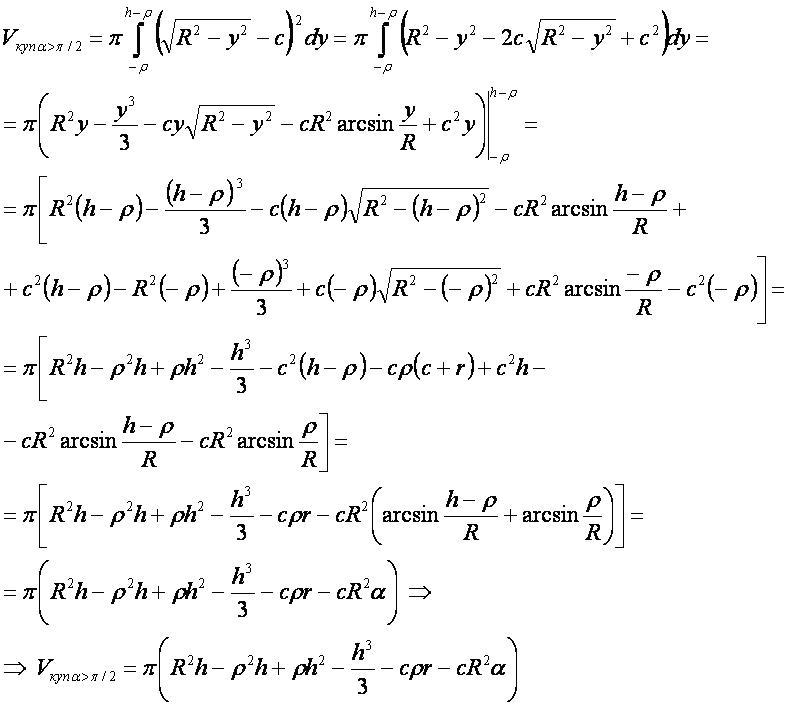Объём купола — различия между версиями
м |
м |
||
| Строка 5: | Строка 5: | ||
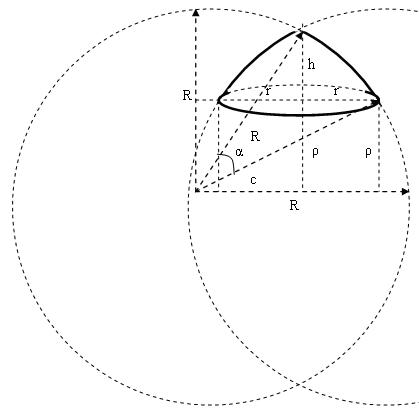
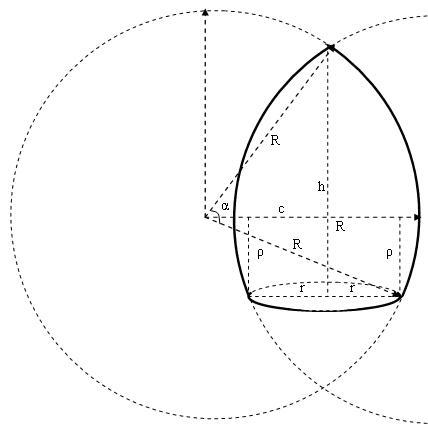
Под '''[[Площадь поверхности купола|куполом]]''' будем подразумевать тело, ограниченное образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения. | Под '''[[Площадь поверхности купола|куполом]]''' будем подразумевать тело, ограниченное образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''R''' — радиус образующей дуги окружности; | '''R''' — радиус образующей дуги окружности; | ||
| Строка 37: | Строка 35: | ||
{{Список ОФВ}} | {{Список ОФВ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 15:26, 18 февраля 2025
Объём купола — это объём, ограниченный образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения.
Под куполом будем подразумевать тело, ограниченное образующей сегмента, вращающегося вокруг оси, проходящей через одну вершину сегмента (под острым углом к диаметру основания сегмента), и плоскостью перпендикулярной оси вращения.
Содержание
Обозначения
R — радиус образующей дуги окружности;
r — радиус основания купола;
ρ — расстояние от основания купола до горизонтальной оси, проходящей через центр образующей окружности;
с — расстояние от центра образующей дуги окружности до вертикальной оси купола;
h — высота купола;
α — угол между радиусами образующей дуги окружности, соединяющими центр с краями образующего сегмента;
Vкуп — объём купола.
Формулы:
Объём купола при α<π/2
Объём купола при α>π/2
Вывод формул:
Объём купола при α<π/2
- Для вывода используется формула 2 "объём фигуры вращения".
- Для нахождения интеграла используется формула 3 "интегралы функций с корнями".
Объём купола при α>π/2
- Для вывода используется формула 2 "объём фигуры вращения".
- Для нахождения интеграла используется формула 3 "интегралы функций с корнями".
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- параболоидное копыто;
- шаровая бочка;
- круговая бочка;
- параболическая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.