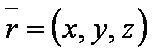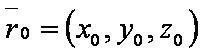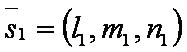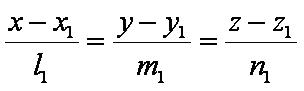Уравнение прямой, проходящей через точку параллельно прямой
Версия от 15:25, 8 февраля 2021; Logic-samara (обсуждение | вклад)
Уравнение прямой, проходящей через точку параллельно прямой, задаётся равенством нулю векторного произведения вектора-разности радиусов-векторов соответствующих точек и направляющего вектора прямой.
Содержание
Обозначения
Введём обозначения:
Формулы:
Координатная форма:
Другие уравнения:
- уравнение прямой, проходящей через две точки;
- уравнение прямой, равноудалённой от трёх точек;
- уравнение прямой, проходящей через точку в направлении вектора;
- уравнение прямой, проходящей через точку параллельно прямой;
- уравнение прямой, проходящей через точку перпендикулярно плоскости;
- уравнение прямой, образованной пересечением двух плоскостей;
- уравнение проекции прямой на плоскость;
- уравнение перпендикуляра из точки к прямой;
- уравнение перпендикуляра из точки к плоскости;
- уравнение перпендикуляра к двум прямым.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.81.
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.223.
- Участник:Logic-samara