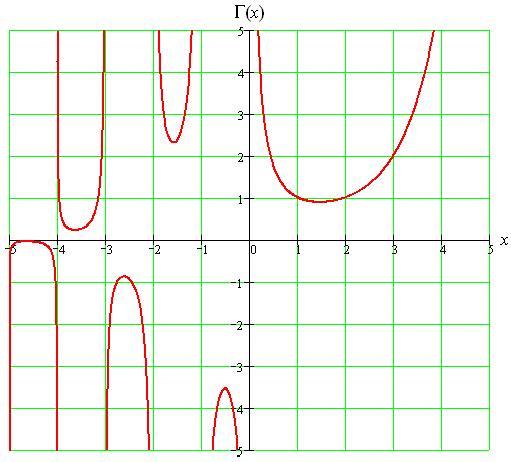
Гамма-функция

Гамма-функция, x=Re(z)

Гамма-функция — это специальная функция от комплексной переменной имеющая интегральное представление, для положительной действительной части аргумента в виде интеграла Эйлера второго рода, для отрицательной действительной части — интегральное представление Ганкеля.

Обозначения

Введём обозначения:

x=Re(z) — действительная часть (абсцисса) числа;

y=Im(z) — мнимая часть (ордината) числа;

z=x+iy — аргумент — комплексное число;

Г(z) — гамма-функция.

Формулы:

Интеграл Эйлера II рода

Интегральное представление Ганкеля

, где

C — контур идёт из -∞ по отрицательной части действительной оси, обходит начало координат в положительном направлении (против часовой стрелки) и опять по отрицательной части оси абсцисс возвращается к исходной точке.

Свойства:

Примеры:

Другие функции:

• многочлен;
• дробно-рациональная функция;
• специальные функции;
• интегральный синус;
• интегральный косинус;
• интегральная показательная функция;
• интегральный логарифм;
• гамма-функция;
• бета-функция;
• неполная гамма-функция;
• неполная бета-функция.

Ссылки

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.633.
• Участник:Logic-samara