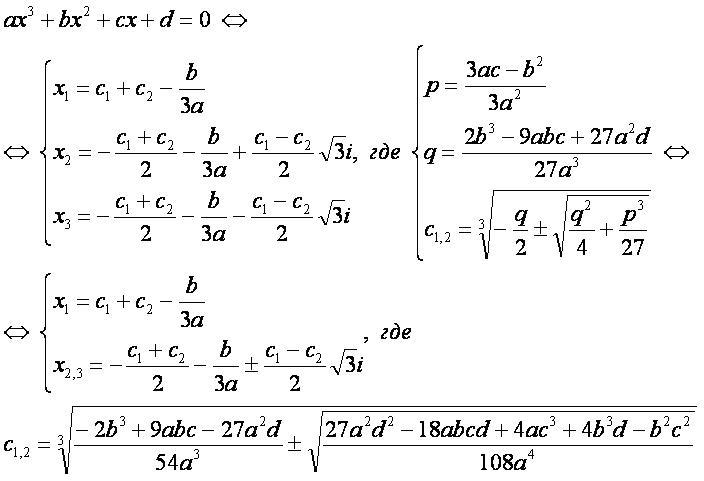Кубическое уравнение
Кубическое уравнение — это такое, которое может быть преобразовано к уравнению с многочленом третьей степени в левой части и нулём в правой части.
Обозначения
x – переменная;
y – дополнительная переменная;
x1, x2, x3 – корни кубического уравнения – комплексные числа;
y1, y2, y3 – корни «неполного» кубического уравнения – комплексные числа;
a, b, c, d, p, q – коэффициенты – действительные числа;
c1, c2 – коэффициенты – комплексные числа;
ax3+bx2+cx+d – многочлен третьей степени, при этом a≠0;
ax3+bx2+cx+d=0 – кубическое уравнение, при этом a≠0;
ay3+py+q=0 – кубическое уравнение «неполного» вида.
Формула
- Кубическое уравнение имеет либо три действительных корня, либо один действительный корень и два комплексных корня.
- Если коэффициенты c1 и c2 - комплексно сопряжённые числа, то их сумма - действительное число, а разность - мнимое число. Соответственно, все три корня кубического уравнения - действительные числа.
- Если коэффициенты c1 и c2 - неравные действительные числа, то два корня кубического уравнения - комлексно сопряжённые числа и один действительный корень.
Вывод формулы
Решение Кардано приведением к «неполному» виду
Другие уравнения:
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.47.