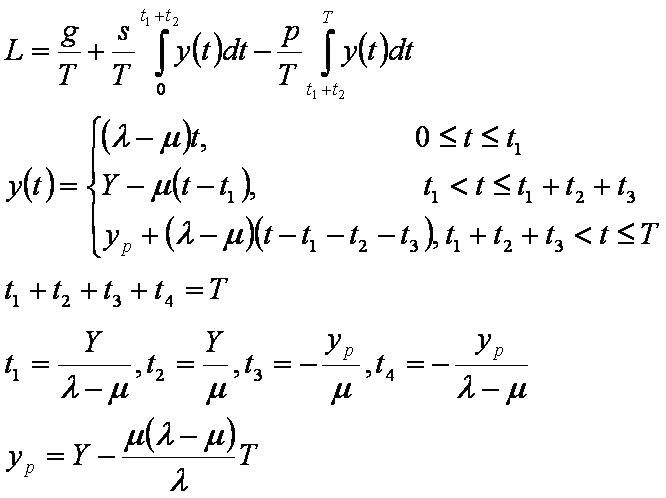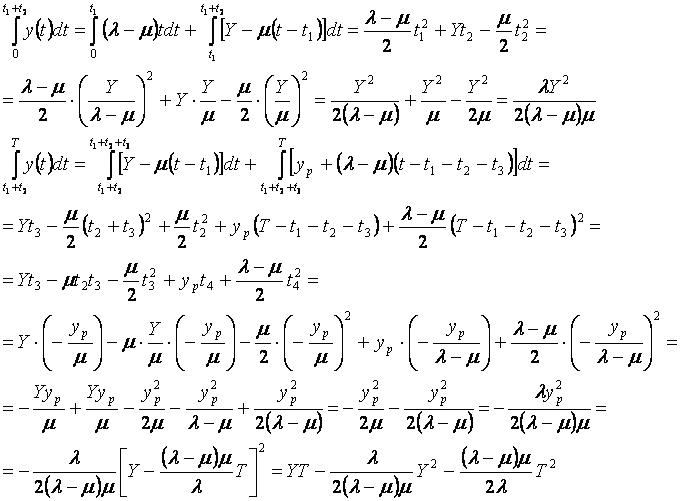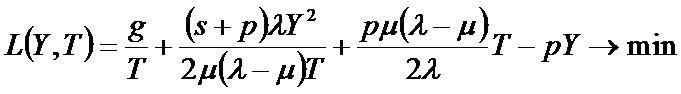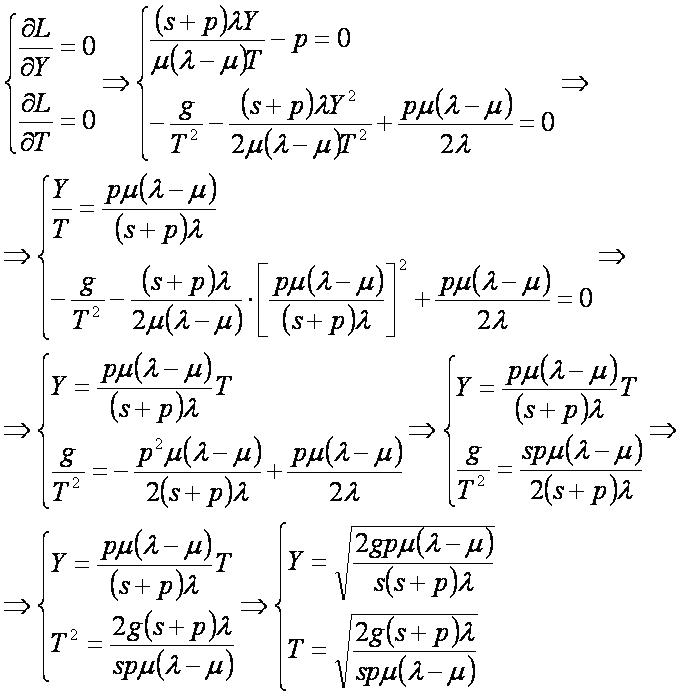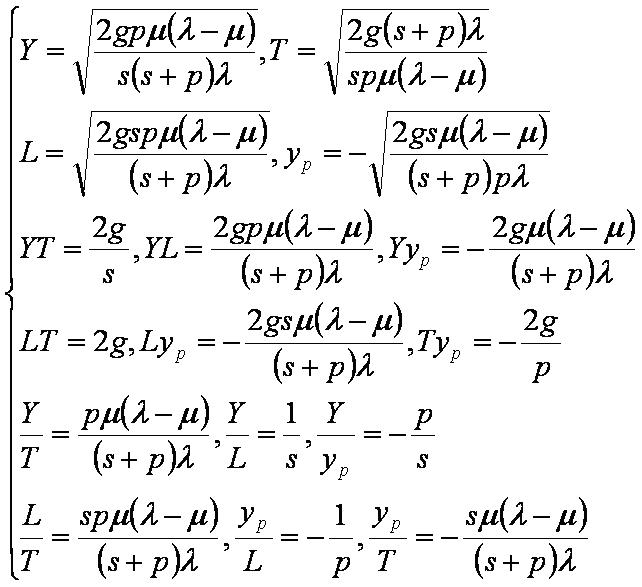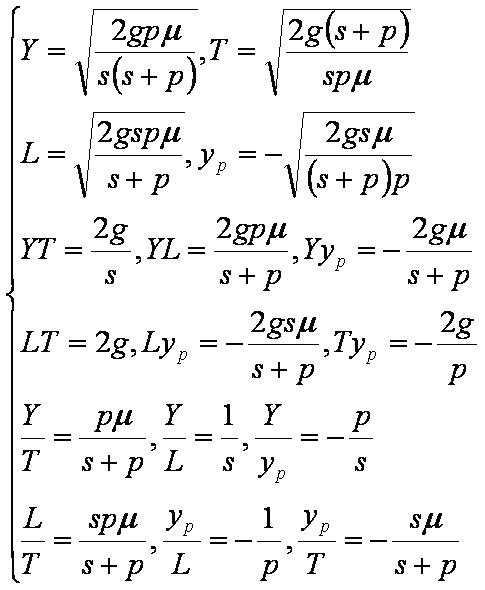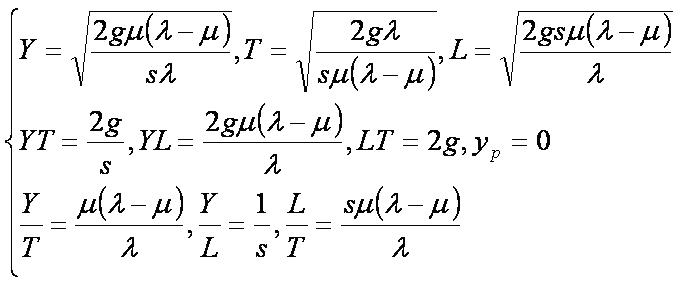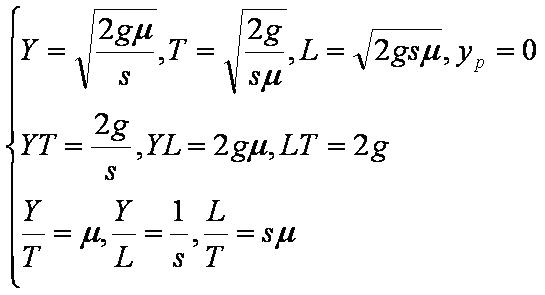Система управления запасами с постоянным спросом

Математическая модель СУЗ с постоянным спросом

Система управления запасами с постоянным спросом — это система, в которой есть поток спроса с постоянной интенсивностью μ и поток поставок запасов с интенсивностью λ.

Графическая модель

Динамическая модель

Динамика изменения запаса за один производственный цикл описывается дифференциальным уравнением:

Соотношения модели имеют вид:

Обозначения

Параметры модели:

Y – предельный запас на складе;

T – время производственного цикла на складе;

L – затраты в единицу времени;

g - фиксированные расходы, связанные с запуском производства;

s – стоимость хранения запаса;

p – штраф за дефицит;

λ – интенсивность поставок;

μ – интенсивность спроса;

t₁ – время пополнения запаса на складе;

t₂ – время расхода запаса на складе;

t₃ – время расхода в условиях дефицита на складе;

t₄ – время пополнения дефицита на складе;

y_p – предельный дефицит на складе;

Приведём формулы основных интегралов:

Учитывая формулы основных интегралов, получаем следующий вид математической модели.

Математическая модель

Для оптимизации модели необходимо найти частные производные и приравнять их нулю:

Решая систему, получаем:

Для оптимального решения верны следующие соотношения:

Рассмотрим различные варианты модели.

Формулы при высокой интенсивности восполнения запаса

При высокой интенсивности восполнения запаса (при λ→∞) получаем формулы и следующие соотношения:

Формулы при высоком штрафе

При высоком штрафе (при p→∞) получаем формулы (приводимые у Хэнссменна) и следующие соотношения:

Формулы Вильсона

При высоком штрафе (при p→∞) и высокой интенсивности восполнения запаса (при λ→∞) получаем формулы Вильсона и следующие соотношения:

Другие системы:

• Система управления запасами;
• Система управления запасами с постоянным спросом;
• Система управления запасами с естественной убылью.

Ссылки

• Рыжиков Ю.И. Управление запасами, «Наука», М.,1969, стр.84-87.
• Участник:Logic-samara