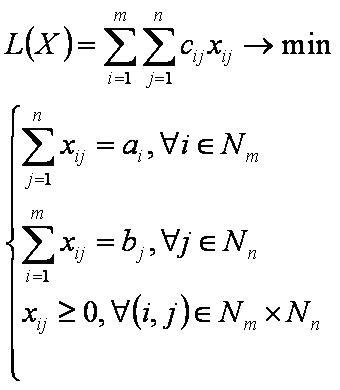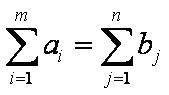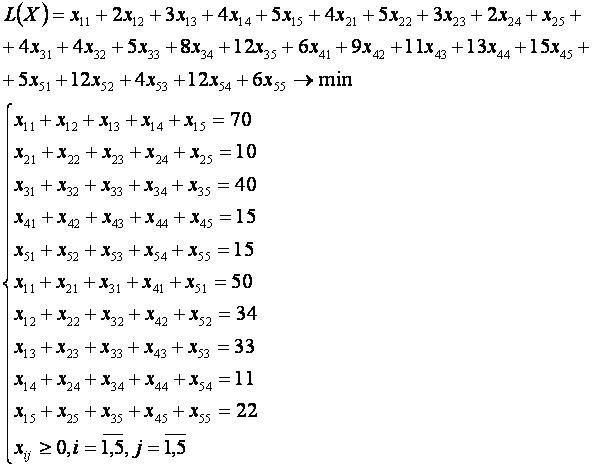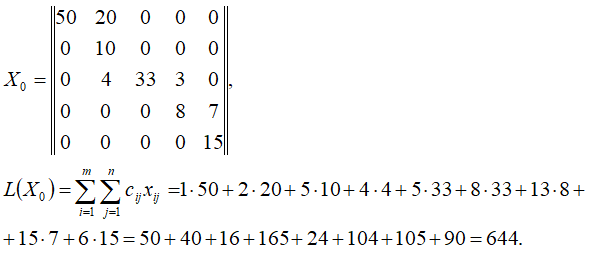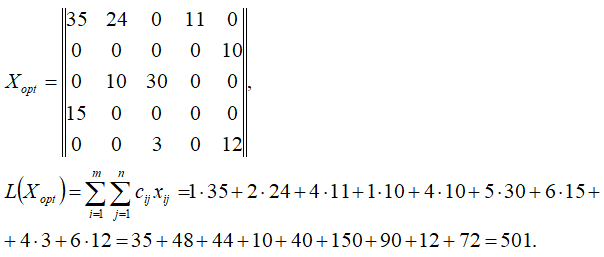Транспортная задача

Математическая модель ТЗ

Транспортная задача – это задача оптимизации перевозок однородных грузов от поставщиков к потребителям.

Постановка задачи

Пусть имеется m поставщиков (A1,A2,…,Am) и n потребителей (B1,B2,…,Bn) однородного продукта. Пусть заданы объёмы поставок a_i продукта поставщиком Ai и объёмы потребностей b_j в продукте у потребителя Bj. Пусть известны транспортные расходы c_ij на перевозку единицы продукта от поставщика Ai к потребителю Bj и необходимо определить план перевозок с минимальной суммой транспортных расходов, тогда классическая транспортная задача (ТЗ) формулируется следующим образом:

,

где x_ij - объём перевозок продукта от поставщика Ai к потребителю Bj.

Транспортную задачу можно представить в виде таблицы

.

Условия разрешимости

Для разрешимости задачи необходимо выполнение условий баланса:

,

т.е. необходимо, чтобы объём поставок продукта равнялся объёму потребностей в нём.

Метод решения

Необходимо найти начальное опорное решение, например, методом северо-западного угла.

Затем транспортная задача решается методом потенциалов.

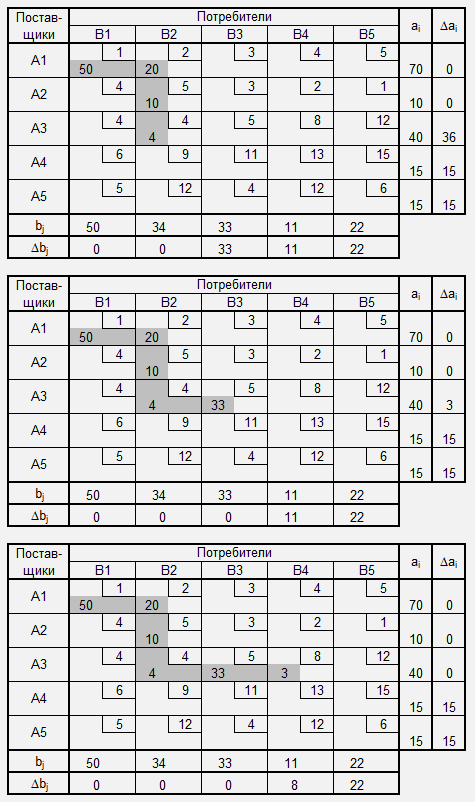
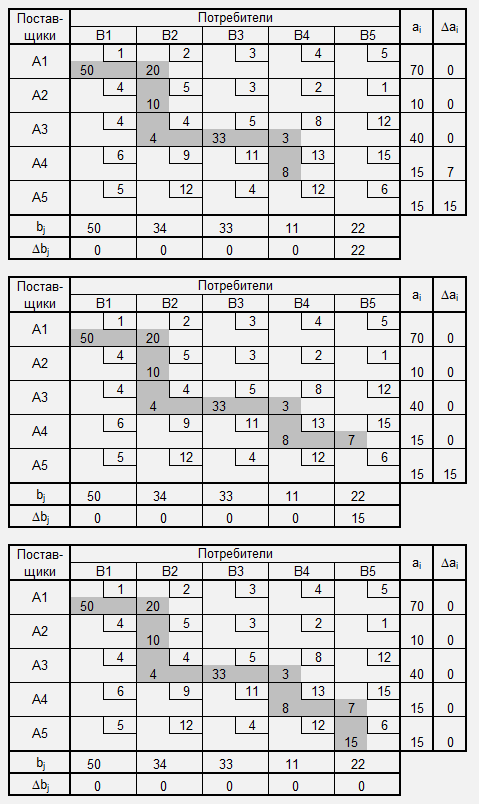
Метод северо-западного угла

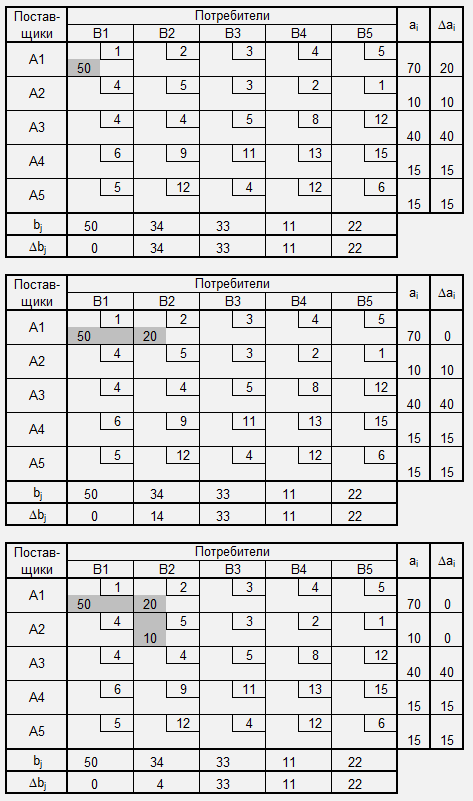
Метод северо-западного угла для нахождения допустимого решения транспортной задачи состоит в последовательном назначении перевозок для клеток транспортной таблицы, находящихся в верхних (северных) строках и в левых (западных) столбцах.

1.Удовлетворяем потребности потребителей (b_j>0) за счёт поставщиков (a_i>0), т.е. назначаем соответствующие перевозки по формулам: x_ij=min(ai,bj), ai=ai-x_ij, b_j=b_j-x_ij.

2.Процесс заполнения клеток (распределения перевозок) для ТЗ продолжается до тех пор пока у поставщиков имеются нераспределённые остатки и у потребителей имеются неудовлетворённые потребности.

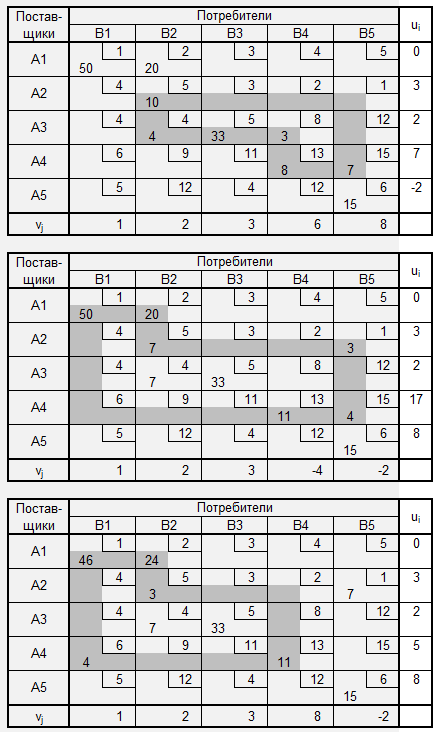
Метод потенциалов

1.Берём решение Xmxn и базис Zmxn, найденные, например, с помощью алгоритма северо-западного угла.

2.Определяем значение целевой функции L=ΣΣc_ijx_ij и базис опорного решения Bo={(i,j)|z_ij=1}.

3.Определяем оценку Δo и элемент (i_o,j_o) с помощью алгоритма расчёта потенциалов и оценок оптимальности.

4.Проверяем решение на оптимальность. Если Δo=0, то решение Xmxn - оптимальное и конец работы.

5.Определяем оценку Δx, элемент (i_x,j_x) и новое опорное решение Xmxn с помощью алгоритма перераспределения перевозок.

6.Определяем новое значение целевой функции L=L-ΔoΔx и новый базис Bo=Bo\(i_x,j_x)U(i_o,j_o). Переходим к пункту 3.

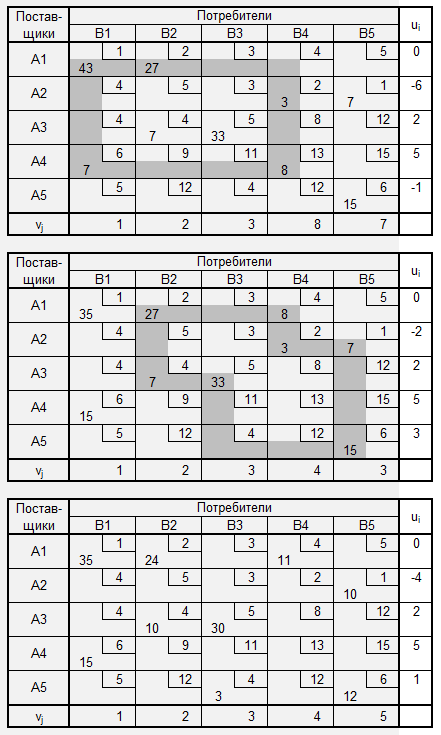
Пример ТЗ

Нахождение допустимого решения методом северо-западного угла

Решение методом потенциалов

Другие задачи:

• Транспортная задача;
• Распределительная задача;
• Задача о назначениях;
• Транспортная задача с промежуточными пунктами;
• Транспортная задача с промежуточными пунктами с запретами;
• Транспортная задача с промежуточными пунктами и ограничением по транзиту;
• Открытая транспортная задача с промежуточными пунктами 1;
• Открытая транспортная задача с промежуточными пунктами 2;
• Открытая транспортная задача с промежуточными пунктами 3;
• Открытая транспортная задача с промежуточными пунктами 4;
• Трёхиндексная транспортная задача.

Ссылки

• Гольштейн Е. Г., Юдин Д. Б. Задачи линейного программирования транспортного типа, М.,1969.
• Участник:Logic-samara