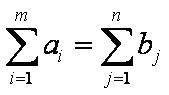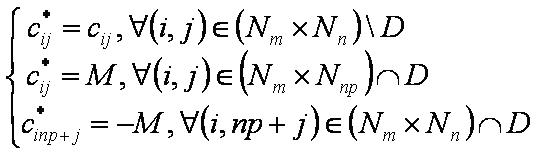Транспортная задача с промежуточными пунктами с запретами

Математическая модель ТЗПП с запретами

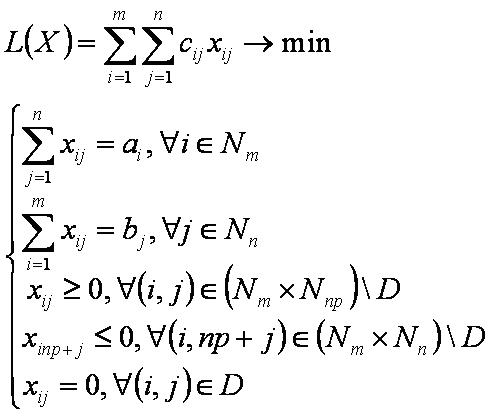
Транспортная задача с промежуточными пунктами с запретами – это транспортная задача оптимизации перевозок с использованием промежуточных (транзитных) пунктов с возможностью запрета отдельных перевозок.

Постановка задачи

В экономической транспортной системе имеются n конечных пунктов (np поставщиков продукции и (n-np) потребителей продукции) и m промежуточных пунктов (складов). Продукция перевозится от поставщиков на склады, будем обозначать эти перевозки положительными переменными x_ij≥0, (i=1,m,j=1,np). А со складов часть продукции перевозится потребителям - их обозначим отрицательными переменными x_ij≤0, (i=1,m,j=np+1,n). Объёмы поставок поставщиков обозначим положительными числами b_j>0, (j=1,np), объёмы потребностей потребителей обозначим отрицательными числами b_j<0, (j=np+1,n). Если склад имеет дополнительные (внутренние) потребности продукции, то обозначим их положительными числами a_i>0, (i=1,mp). Если склад имеет излишки продукции или нулевые остатки, то обозначим их числами a_i≤0, (i=mp+1,m). Транспортные тарифы на перевозку единицы продукции от поставщика на склад выразим положительными числами c_ij>0, (i=1,m,j=1,np), транспортные тарифы на перевозку со склада к потребителю выразим отрицательными числами c_ij<0, (i=1,m,j=np+1,n).

Пусть D – это множество запрещённых перевозок (коммуникаций), оно содержит k элементов (запретов), D={(i_t, j_t),t=1,k}.

Тогда математическая модель задачи с запретами принимает вид:

,

где x_ij — объём перевозок продукта между промежуточным пунктом Ai и конечным пунктом Bj.

Условия разрешимости

Для разрешимости задачи с запретами необходимо выполнение условий баланса:

,

то есть необходимо, чтобы алгебраическая сумма поставок на склады и отрицательных поставок со складов (потребностей в продукции) равнялась алгебраической сумме дополнительных потребностей в продукции на складах. Но для задачи с запретами решение может отсутствовать, например, если запретов слишком много. Следовательно, условия баланса не являются достаточными.

Постановка вспомогательной задачи

Для построения вспомогательной задачи введём новые обозначения:

M — это достаточно большое положительное число.

.

Математическая модель вспомогательной задачи принимает следующий вид:

.

Решение вспомогательной задачи

Очевидно, что вспомогательная задача является закрытой транспортной задачей с промежуточными пунктами, которая разрешима по построению. Для определения начального решения используется метод северо-западного угла, а для решения применяется метод потенциалов. M-множители и метод потенциалов приводят к нулевым запретным перевозкам в оптимальном решении. Если все запретные перевозки в оптимальном решении вспомогательной задачи равны нулю, то исходная задача с запретами решена, если нет, то исходная задача с запретами не имеет решения.

Для более эффективного решения ТЗПП с запретами, предлагается эвристический алгоритм решения ТЗПП с запретами, в котором M-множители заменяются на конкретные числа.

Другие задачи:

• Транспортная задача;
• Распределительная задача;
• Задача о назначениях;
• Транспортная задача с промежуточными пунктами;
• Транспортная задача с промежуточными пунктами с запретами;
• Транспортная задача с промежуточными пунктами и ограничением по транзиту;
• Открытая транспортная задача с промежуточными пунктами 1;
• Открытая транспортная задача с промежуточными пунктами 2;
• Открытая транспортная задача с промежуточными пунктами 3;
• Открытая транспортная задача с промежуточными пунктами 4;
• Трёхиндексная транспортная задача.

Ссылки

• Krivopalov V. Y., Krivopalov Y. A. The potential method for solving the transportation problem with transit points. New Magenta Papers. Magenta Technology, 2013. — Vol.2 — P.31-38.
• Кривопалов В. Ю., Метод северо-западного угла для нахождения допустимого решения транспортной задачи с промежуточными пунктами. Сборник конференции ПИТ-2014, СГАУ, стр.369-372. http://www.ssau.ru/files/events/2014/pit_14_1_6.pdf
• Кривопалов В. Ю., Обобщённый метод потенциалов для решения транспортной задачи с промежуточными пунктами. Сборник Х конференции «Наука. Творчество» 2014, Самара-Москва, Т.1,стр.23-29.
• Кривопалов В. Ю., Решение транспортной задачи с промежуточными пунктами с запретами. Сборник ХI конференции «Наука. Творчество» 2015, Самара, Т.1,стр.22-27.
• Участник:Logic-samara