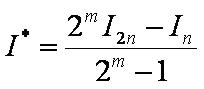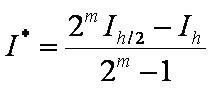Численное интегрирование

Численное интегрирование — это способ вычисления определённого интеграла по формуле.

Численное интегрирование

Описание

Суть численного интегрирования состоит в расчёте значения определённого интеграла по взвешенным значениям подынтегральной функции, без использования первообразной функции.

Сила численного интегрирования состоит в возможности оценки значения определённого интеграла путём простых вычислений.

Формула

При численном интегрировании используется общая формула определённого интеграла. , где

– квадратурная формула,

x_i – некоторые точки отрезка [a,b],

n – число отрезков на [a,b],

f(x_i) – значения подынтегральной функции в точках x_i,

q_i – весовые коэффициенты,

R_n – остаточный член.

Порядок точности формул

• m=1 для формул левых и правых прямоугольников
• m=2 для формул прямоугольников и трапеций
• m=4 для формул Симпсона и трёх восьмых

Правило Рунге

Для оценки точности расчёта интеграла I с помощью квадратурных формул (например, необходимо рассчитать значение интеграла с помощью квадратурной формулы для I_2n=I_h/2) на практике можно применять правило Рунге:

или , где

I_n=I_h – значение квадратурной формулы при шаге h=(b-a)/n,

I_2n=I_h/2 – значение квадратурной формулы при шаге h/2=(b-a)/(2n),

m – порядок точности квадратурной формулы.

Условие применения правила Рунге строго задаётся для чётного n следующим неравенством:

или , где

I_n=I_h – значение квадратурной формулы при шаге h=(b-a)/n,

I_2n=I_h/2 – значение квадратурной формулы при шаге h/2=(b-a)/(2n),

I_n/2=I_2h – значение квадратурной формулы при шаге 2h=(b-a)/(n/2),

m – порядок точности квадратурной формулы.

Формула Ричардсона

Более точным (по крайней мере на порядок выше, т.е. с порядком точности m+1) значением интеграла I (по сравнению со значением I_2n=I_h/2) является значение I*, вычисленное или экстраполированное по формуле Ричардсона:

или , где

I_n=I_h – значение квадратурной формулы при шаге h=(b-a)/n,

I_2n=I_h/2 – значение квадратурной формулы при шаге h/2=(b-a)/(2n),

m – порядок точности квадратурной формулы.

Примеры формул:

• формула правых прямоугольников;
• формула левых прямоугольников;
• формула прямоугольников;
• формула трапеций;
• формула Симпсона;
• формула трёх восьмых.

Численные методы:

• решение уравнений;
• решение систем уравнений;
• ортогонализация;
• решение дифференциальных уравнений;
• аппроксимация;
• интерполяция;
• численное интегрирование;
• нахождение экстремумов.

Ссылки

• Демидович Б.П., Марон И.А. Основы вычислительной математики. М.: Наука, 1970.
• Участник:Logic-samara