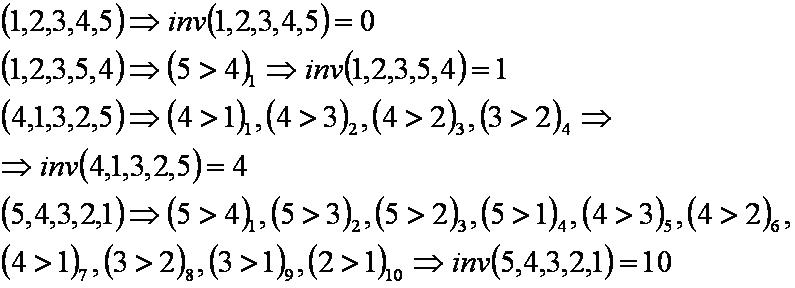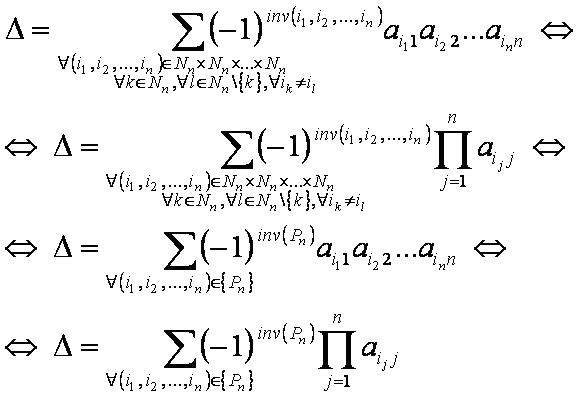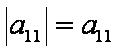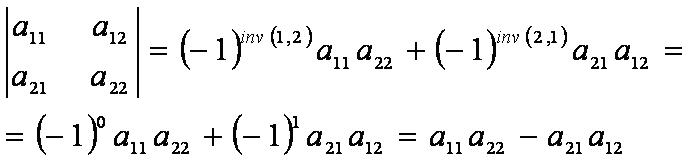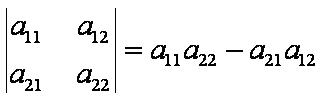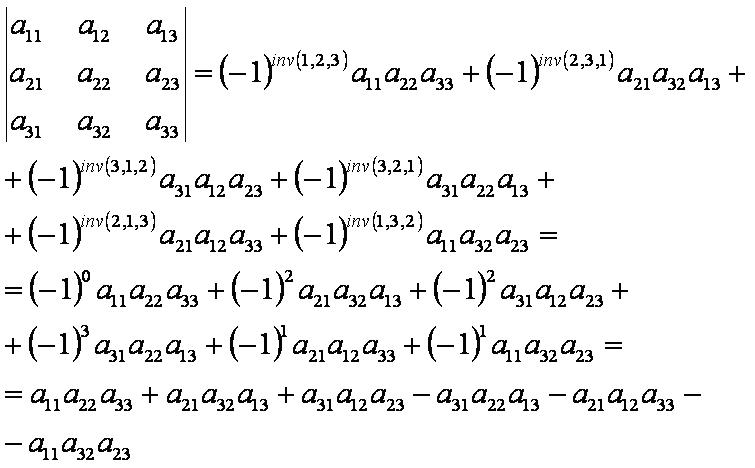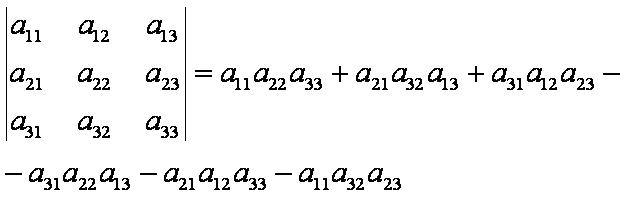Определитель
Определитель матрицы — это число равное алгебраической сумме всевозможных произведений n элементов матрицы размерности nxn, не лежащих в одной строке и в одном столбце, причём произведения берутся со знаком, определяемым по числу инверсий (для чётного числа инверсий знак "+", для нечётного числа инверсий знак "-").
Содержание
Обозначения
n – порядок матрицы;
nxn – размерность матрицы;
aij – элемент матрицы, лежащий на пересечении i-ой строки и j-ого столбца матрицы;
Инверсия
Инверсией называется нарушение порядка (возрастания) в наборе индексов (чисел в перестановке).
Число инверсий – это число всех нарушений порядка (возрастания) в наборе индексов (чисел в перестановке).
– число инверсий перестановки или набора индексов.
Примеры:
Формулы:
- Заметим, что определитель существует только для квадратных матриц.
Примеры:
Определитель 1-ого порядка
- Заметим, что |a11| - это не модуль числа, а определитель матрицы из одного элемента.
Определитель 2-ого порядка
Определитель 3-его порядка
Отсюда следует формула вида:
Другие операции:
- сложение матриц;
- вычитание матриц;
- умножение матрицы на число;
- умножение матриц;
- умножение элементов матриц;
- деление элементов матриц;
- возведение в квадрат элементов матрицы;
- извлечение корня из элементов матрицы;
- деление матриц;
- транспонирование матрицы;
- обращение матрицы;
- обращение клеточной матрицы;
- возведение в степень матрицы;
- нахождение определителя;
- нахождение минора;
- нахождение алгебраического дополнения.