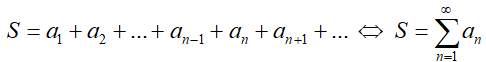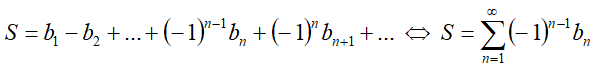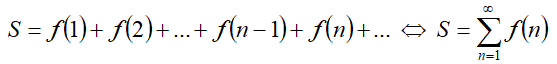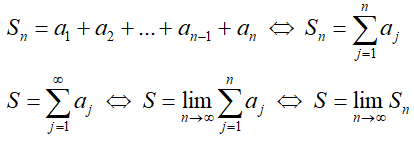Ряд — различия между версиями
м |
м |
||
| (не показано 13 промежуточных версий этого же участника) | |||
| Строка 2: | Строка 2: | ||
= Ряд = | = Ряд = | ||
== Формула == | == Формула == | ||
| − | [[файл:РЯД01. | + | [[файл:РЯД01.png]] |
Слагаемые ряда '''a<sub>n</sub>''' называются членами ряда. | Слагаемые ряда '''a<sub>n</sub>''' называются членами ряда. | ||
| Строка 8: | Строка 8: | ||
'''Знакопеременными''' называются ряды, члены которых поочерёдно имеют то положительный, то отрицательный знаки. Общий вид знакопеременного ряда задаётся следующей формулой: | '''Знакопеременными''' называются ряды, члены которых поочерёдно имеют то положительный, то отрицательный знаки. Общий вид знакопеременного ряда задаётся следующей формулой: | ||
| − | [[файл: | + | [[файл:РЯД011.png]] |
| − | Если члены ряда | + | Если члены ряда — числа, то ряд называется '''числовым''', если же они являются функциями (причём каждый член ряда определяется отдельной функцией '''f<sub>n</sub>(x)'''), то ряд называется '''функциональным'''. Члены числового ряда определяются одной функцией от числа '''f(n)''', например: |
| + | |||
| + | [[файл:РЯД012.png]] | ||
Сумма первых '''n''' членов называется '''частичной суммой S<sub>n</sub>'''. | Сумма первых '''n''' членов называется '''частичной суммой S<sub>n</sub>'''. | ||
| − | [[файл:РЯД02. | + | [[файл:РЯД02.png]] |
'''Сходимость ряда''' | '''Сходимость ряда''' | ||
| − | Числовой ряд называется '''сходящимся''', если существует конечный предел последовательности его частичных сумм | + | Числовой ряд называется '''сходящимся''', если существует конечный предел последовательности его частичных сумм — этот предел называется суммой ряда; в противном случае ряд называется '''расходящимся'''. |
== [[Признаки сходимости]]: == | == [[Признаки сходимости]]: == | ||
{{Список При}} | {{Список При}} | ||
| − | '''[[Необходимый признак]]''' используется для определения расходимости ряда [[файл: | + | '''[[Необходимый признак]]''' используется для определения расходимости ряда [[файл:РЯД00.png]], при условии [[файл:РЯД031.png]]. |
| − | '''[[Признак сравнения]]''' используется или для определения сходимости меньшего (доминируемого) ряда [[файл: | + | '''[[Признак сравнения]]''' используется или для определения сходимости меньшего (доминируемого) ряда [[файл:РЯД00.png]] или для определения расходимости большего (доминирующего) ряда [[файл:РЯД000.png]], при условии [[файл:РЯД032.png]]. |
| − | '''[[Признак Даламбера]]''' используется для определения сходимости или расходимости ряда [[файл: | + | '''[[Признак Даламбера]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии [[файл:РЯД033.png]]. |
| − | '''[[Радикальный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл: | + | '''[[Радикальный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии [[файл:РЯД034.png]]. |
| − | '''[[Интегральный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл: | + | '''[[Интегральный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии существования интеграла интегрируемой функции [[файл:РЯД035.png]]. |
| − | '''[[Признак Раабе]]''' используется для определения сходимости или расходимости ряда [[файл: | + | '''[[Признак Раабе]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии [[файл:РЯД036.png]]. |
| − | '''[[Признак Лейбница]]''' используется для определения сходимости знакопеременного ряда [[файл: | + | '''[[Признак Лейбница]]''' используется для определения сходимости знакопеременного ряда [[файл:РЯД001.png]], при условии [[файл:РЯД037.png]]. |
| − | == | + | == [[Математический анализ|Другие ряды:]] == |
{{Список Ряд}} | {{Список Ряд}} | ||
= [[Математический анализ|Другие понятия:]] = | = [[Математический анализ|Другие понятия:]] = | ||
| Строка 41: | Строка 43: | ||
= Ссылки = | = Ссылки = | ||
*Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975. | *Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975. | ||
| − | |||
[[Категория:Математика]] | [[Категория:Математика]] | ||
Текущая версия на 10:14, 18 февраля 2025
Ряд — это бесконечная последовательность слагаемых или бесконечная сумма членов последовательности.
Ряд[править]
Формула[править]
Слагаемые ряда an называются членами ряда.
Знакопеременными называются ряды, члены которых поочерёдно имеют то положительный, то отрицательный знаки. Общий вид знакопеременного ряда задаётся следующей формулой:
Если члены ряда — числа, то ряд называется числовым, если же они являются функциями (причём каждый член ряда определяется отдельной функцией fn(x)), то ряд называется функциональным. Члены числового ряда определяются одной функцией от числа f(n), например:
Сумма первых n членов называется частичной суммой Sn.
Сходимость ряда
Числовой ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм — этот предел называется суммой ряда; в противном случае ряд называется расходящимся.
Признаки сходимости:[править]
Необходимый признак используется для определения расходимости ряда 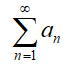 , при условии
, при условии 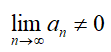 .
.
Признак сравнения используется или для определения сходимости меньшего (доминируемого) ряда 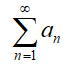 или для определения расходимости большего (доминирующего) ряда
или для определения расходимости большего (доминирующего) ряда 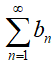 , при условии
, при условии ![]() .
.
Признак Даламбера используется для определения сходимости или расходимости ряда 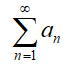 , при условии
, при условии 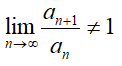 .
.
Радикальный признак Коши используется для определения сходимости или расходимости ряда 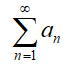 , при условии
, при условии 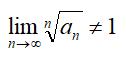 .
.
Интегральный признак Коши используется для определения сходимости или расходимости ряда 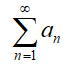 , при условии существования интеграла интегрируемой функции
, при условии существования интеграла интегрируемой функции 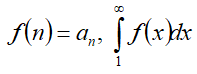 .
.
Признак Раабе используется для определения сходимости или расходимости ряда 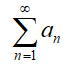 , при условии
, при условии 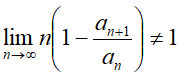 .
.
Признак Лейбница используется для определения сходимости знакопеременного ряда 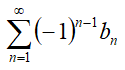 , при условии
, при условии ![]() .
.
Другие ряды:[править]
Другие понятия:[править]
Ссылки[править]
- Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975.