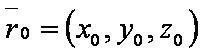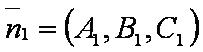Уравнение перпендикуляра из точки к плоскости — различия между версиями
м |
м |
||
| Строка 1: | Строка 1: | ||
'''Уравнение перпендикуляра из точки к плоскости''' — это уравнение прямой, проходящей через точку в направлении нормали к плоскости, задаётся равенством нулю [[Векторное произведение|векторного произведения]] [[вектор]]а-разности радиусов-векторов точек и нормали к плоскости. | '''Уравнение перпендикуляра из точки к плоскости''' — это уравнение прямой, проходящей через точку в направлении нормали к плоскости, задаётся равенством нулю [[Векторное произведение|векторного произведения]] [[вектор]]а-разности радиусов-векторов точек и нормали к плоскости. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
[[файл:ВЕК79.JPG]] — радиус-вектор точки перпендикуляра; | [[файл:ВЕК79.JPG]] — радиус-вектор точки перпендикуляра; | ||
| Строка 23: | Строка 21: | ||
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | ||
*Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1964, стр.185. | *Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1964, стр.185. | ||
| − | |||
[[Категория:Математика]][[Категория:Уравнения]] | [[Категория:Математика]][[Категория:Уравнения]] | ||
Текущая версия на 13:39, 18 февраля 2025
Уравнение перпендикуляра из точки к плоскости — это уравнение прямой, проходящей через точку в направлении нормали к плоскости, задаётся равенством нулю векторного произведения вектора-разности радиусов-векторов точек и нормали к плоскости.
Содержание
Обозначения
— радиус-вектор точки перпендикуляра;
— радиус-вектор точки;
— нормаль к плоскости;
— уравнение плоскости.
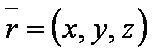
Формулы:
Векторная форма:
Координатная форма:
- Заметим, что формулы уравнения перпендикуляра из точки к плоскости аналогичны формулам уравнения прямой, проходящей через точку перпендикулярно плоскости.
Другие уравнения:
- уравнение прямой, проходящей через две точки;
- уравнение прямой, равноудалённой от трёх точек;
- уравнение прямой, проходящей через точку в направлении вектора;
- уравнение прямой, проходящей через точку параллельно прямой;
- уравнение прямой, проходящей через точку перпендикулярно плоскости;
- уравнение прямой, образованной пересечением двух плоскостей;
- уравнение проекции прямой на плоскость;
- уравнение перпендикуляра из точки к прямой;
- уравнение перпендикуляра из точки к плоскости;
- уравнение перпендикуляра к двум прямым.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Выгодский М.Я. Справочник по высшей математике. М.: Наука, 1964, стр.185.
