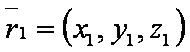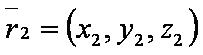Проекция вектора на вектор — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 3: | Строка 3: | ||
'''Векторная проекция вектора на другой вектор''' (в геометрическом смысле) — это вектор с длиной, равной отношению скалярного произведения этих векторов к длине второго вектора, и с направлением второго вектора. | '''Векторная проекция вектора на другой вектор''' (в геометрическом смысле) — это вектор с длиной, равной отношению скалярного произведения этих векторов к длине второго вектора, и с направлением второго вектора. | ||
== Обозначения == | == Обозначения == | ||
| − | + | [[файл:ВЕК71.JPG]] — первый вектор; | |
| − | [[файл: | + | [[файл:ВЕК72.JPG]] — второй вектор. |
| − | |||
| − | |||
== Формулы == | == Формулы == | ||
[[файл:ПВВ01.JPG]] | [[файл:ПВВ01.JPG]] | ||
| Строка 17: | Строка 15: | ||
== Ссылки == | == Ссылки == | ||
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 09:32, 19 февраля 2025
Числовая проекция вектора на другой вектор (в алгебраическом смысле) — это число, равное отношению скалярного произведения этих векторов к длине второго вектора.
Векторная проекция вектора на другой вектор (в геометрическом смысле) — это вектор с длиной, равной отношению скалярного произведения этих векторов к длине второго вектора, и с направлением второго вектора.
Содержание
Обозначения
— первый вектор;
— второй вектор.
Формулы
- При r2=r1 получаем равенства
Другие формулы:
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
