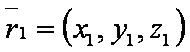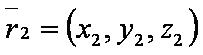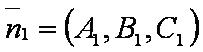Точка, равноудалённая от четырёх точек — различия между версиями
(начало) |
м |
||
| Строка 3: | Строка 3: | ||
Введём обозначения: | Введём обозначения: | ||
| − | [[файл: | + | [[файл:ВЕК79.JPG]] — радиус-[[вектор]] равноудалённой точки; |
| − | [[файл: | + | [[файл:ВЕК71.JPG]] — радиус-вектор первой точки; |
| − | [[файл: | + | [[файл:ВЕК72.JPG]] — радиус-вектор второй точки; |
| − | [[файл: | + | [[файл:ВЕК73.JPG]] — радиус-вектор третьей точки; |
| − | [[файл: | + | [[файл:ВЕК74.JPG]] — радиус-вектор четвёртой точки; |
| − | [[файл: | + | [[файл:ВЕК91.JPG]] — нормаль к первой плоскости; |
| − | [[файл: | + | [[файл:ВЕК92.JPG]] — нормаль ко второй плоскости; |
| − | [[файл: | + | [[файл:ВЕК93.JPG]] — нормаль к третьей плоскости; |
[[файл:ПЛО01.JPG]] — уравнение первой плоскости; | [[файл:ПЛО01.JPG]] — уравнение первой плоскости; | ||
Версия 16:11, 8 февраля 2021
Точка, равноудалённая от четырёх точек, — это точка, образованная пересечением трёх равноудалённых плоскостей, для пар одной точки с другими точками (при однозначном определении равноудалённой плоскости для двух точек).
Содержание
Обозначения
Введём обозначения:
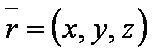
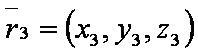
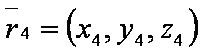
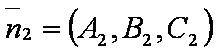
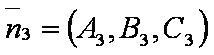
— уравнение третьей плоскости.
Формулы:
Векторная форма:
Координатная форма:
- Заметим, что равноудалённая точка является центром сферы, проходящей через заданные четыре точки.
Другие формулы:
- Основание перпендикуляра из точки к прямой;
- Основание перпендикуляра из точки к плоскости;
- Точка пересечения перпендикуляра к двум прямым с первой прямой;
- Точка пересечения перпендикуляра к двум прямым со второй прямой;
- Точка пересечения прямой и плоскости;
- Точка пересечения трёх плоскостей;
- Точка, равноудалённая от двух прямых;
- Точка, равноудалённая от четырёх точек;
- Точка деления отрезка в данном отношении;
- Точка прямой, находящаяся от первой точки прямой до второй в данном отношении;
- Точка прямой, находящаяся перед первой точкой прямой до второй в данном отношении;
- Точка прямой, находящаяся от первой точки прямой за второй в данном отношении.