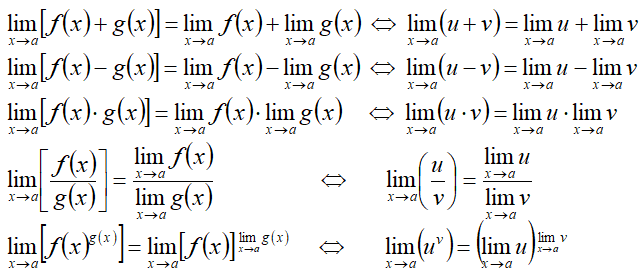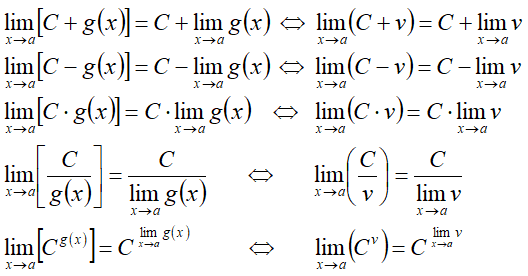Предел

Предел — это некоторая величина, к которой стремится бесконечная последовательность или функция. Соответственно, различают предел последовательности и предел функции (в точке, на бесконечности). Считается также, что предел может быть равен бесконечности.

Пределы

Предел последовательности

Пределом числовой последовательности {x_n} называется число A, в ε-окрестность которого попадают все члены последовательности с номером больше номера N(ε).

Виды пределов

Свойства пределов

Для последовательностей {x_n} и {y_n} верны правила:

При x_n и y_n=C получаем:

При x_n=C и y_n получаем:

Предел функции

Пределом функции f{x} в точке a называется число A, в ε-окрестность которого попадают все значения функции в точках из δ-окрестности точки a.

Виды пределов

Свойства пределов

Для функций u=f(x) и v=g(x) верны правила:

При f(x) и g(x)=C получаем:

При f(x)=C и g(x) получаем:

Замечательные пределы:

• первый замечательный предел
• второй замечательный предел

Приёмы нахождения пределов:

• пределы дробно-рациональных функций;
• пределы функций с корнями;
• пределы с использованием 2ЗП.

Другие понятия:

• число;
• формулы;
• погрешность;
• предел;
• производная;
• дифференциал;
• последовательность;
• ряд;
• признак сходимости;
• интеграл;
• преобразование;
• экстремум;
• вектор;
• матрица;
• функции;
• уравнения;
• дифференциальные уравнения.

Ссылки

• Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.