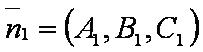Уравнение прямой, образованной пересечением двух плоскостей — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Уравнение прямой, образованной пересечением двух плоскостей,''' — это уравнение прямой, проходящей через точки принадлежащие обеим плоскостям. | '''Уравнение прямой, образованной пересечением двух плоскостей,''' — это уравнение прямой, проходящей через точки принадлежащие обеим плоскостям. | ||
== Обозначения == | == Обозначения == | ||
| − | + | [[файл:ВЕК79.JPG]] — радиус-[[вектор]] точки прямой; | |
| − | [[файл: | + | [[файл:ВЕК91.JPG]] — нормаль к первой плоскости; |
| − | |||
| − | |||
| − | [[файл: | + | [[файл:ВЕК92.JPG]] — нормаль ко второй плоскости; |
[[файл:ПЛО01.JPG]] — уравнение первой плоскости; | [[файл:ПЛО01.JPG]] — уравнение первой плоскости; | ||
| Строка 23: | Строка 21: | ||
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | ||
*Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.222. | *Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.222. | ||
| − | |||
[[Категория:Математика]][[Категория:Уравнения]] | [[Категория:Математика]][[Категория:Уравнения]] | ||
Текущая версия на 13:41, 18 февраля 2025
Уравнение прямой, образованной пересечением двух плоскостей, — это уравнение прямой, проходящей через точки принадлежащие обеим плоскостям.
Содержание
Обозначения
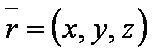
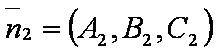
Формулы:
Другие уравнения:
- уравнение прямой, проходящей через две точки;
- уравнение прямой, равноудалённой от трёх точек;
- уравнение прямой, проходящей через точку в направлении вектора;
- уравнение прямой, проходящей через точку параллельно прямой;
- уравнение прямой, проходящей через точку перпендикулярно плоскости;
- уравнение прямой, образованной пересечением двух плоскостей;
- уравнение проекции прямой на плоскость;
- уравнение перпендикуляра из точки к прямой;
- уравнение перпендикуляра из точки к плоскости;
- уравнение перпендикуляра к двум прямым.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.222.