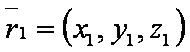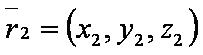Площадь поверхности тетраэдра — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 4: | Строка 4: | ||
'''Тетраэдр''' — это четырёхгранник с гранями из [[Площадь треугольника|треугольников]]. | '''Тетраэдр''' — это четырёхгранник с гранями из [[Площадь треугольника|треугольников]]. | ||
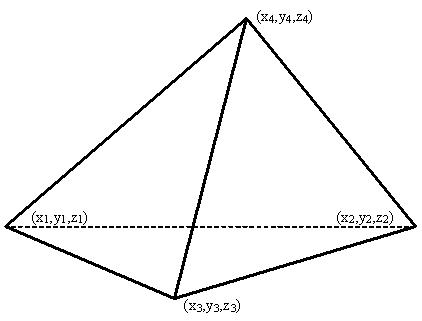
== Обозначения == | == Обозначения == | ||
| − | + | [[файл:ВЕК71.JPG]] — радиус-вектор первой точки; | |
| − | [[файл: | + | [[файл:ВЕК72.JPG]] — радиус-вектор второй точки; |
| − | [[файл: | + | [[файл:ВЕК73.JPG]] — радиус-вектор третьей точки; |
| − | [[файл: | + | [[файл:ВЕК74.JPG]] — радиус-вектор четвёртой точки; |
| − | [[файл: | + | [[файл:ВЕК99.JPG]] — нормаль к плоскости, проходящей через три заданные точки; |
| − | |||
| − | |||
'''S<sub>Δ</sub>''' — площадь грани тетраэдра, построенной по трём заданным точкам; | '''S<sub>Δ</sub>''' — площадь грани тетраэдра, построенной по трём заданным точкам; | ||
| Строка 28: | Строка 26: | ||
{{Список ПМГ}} | {{Список ПМГ}} | ||
== Ссылки == | == Ссылки == | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 16:22, 18 февраля 2025
Площадь поверхности тетраэдра — это число, характеризующее тетраэдр в единицах измерения площади, равное сумме площадей его (тетраэдра) граней.
Тетраэдр — это четырёхгранник с гранями из треугольников.
Содержание
Обозначения
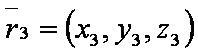
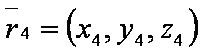
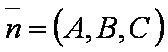
SΔ — площадь грани тетраэдра, построенной по трём заданным точкам;
Sтетр — площадь поверхности тетраэдра, построенного по четырём заданным точкам.
Формулы:
где