Доверительный интервал средней при известной дисперсии — различия между версиями
м |
м |
||
| Строка 23: | Строка 23: | ||
<!--[[файл:ДИСД01.JPG]]--> | <!--[[файл:ДИСД01.JPG]]--> | ||
[[файл:ДИСД01.png]] | [[файл:ДИСД01.png]] | ||
| + | *Заметим, что '''u<sub>1-α/2</sub>=-u<sub>α/2</sub>'''. | ||
== [[Доверительные интервалы|Другие формулы:]] == | == [[Доверительные интервалы|Другие формулы:]] == | ||
{{Список ДИнт}} | {{Список ДИнт}} | ||
Версия 15:32, 6 апреля 2025
Доверительный интервал средней при известной дисперсии — это интервал, которому принадлежит с вероятностью (1-α) значение средней нормально распределённой случайной величины X в генеральной совокупности.
Обозначения
n — число значений в выборке;
![]() — средняя генеральной совокупности X;
— средняя генеральной совокупности X;
σГ=σ — среднеквадратическое отклонение генеральной совокупности;
DГ=σ2 — дисперсия генеральной совокупности;
α — уровень значимости;
γ=1-α — коэффициент доверия — вероятность попадания в доверительный интервал;
u — статистика, распределённая по нормальному закону N(0;1);
 — интегральная функция нормального закона распределения стандартизованной случайной величины;
— интегральная функция нормального закона распределения стандартизованной случайной величины;
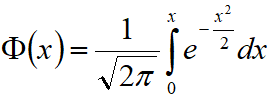 — интегральная функция Лапласа, отличается от интегральной функции нормального закона для стандартизованной случайной величины на 0,5, т.е. Ф(x)=F(x)-0,5.
— интегральная функция Лапласа, отличается от интегральной функции нормального закона для стандартизованной случайной величины на 0,5, т.е. Ф(x)=F(x)-0,5.
Доверительный интервал
- Заметим, что u1-α/2=-uα/2.
Другие формулы:
- Доверительный интервал средней при известной дисперсии;
- Доверительный интервал средней при неизвестной дисперсии;
- Доверительный интервал дисперсии при известной средней;
- Доверительный интервал дисперсии при неизвестной средней;
- Доверительный интервал коэффициента корреляции;
- Доверительный интервал вероятности в испытаниях Бернулли.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970, стр.562.

