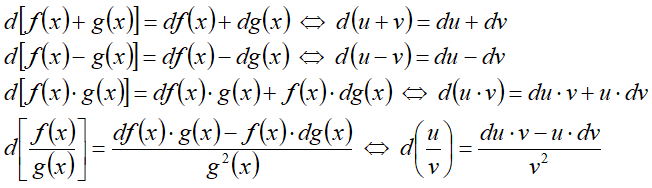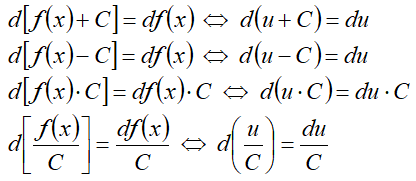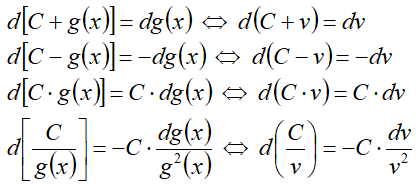Дифференциал — различия между версиями
| Строка 9: | Строка 9: | ||
Нахождение дифференциала функции называется дифференцированием, так как требует нахождения производной. | Нахождение дифференциала функции называется дифференцированием, так как требует нахождения производной. | ||
| + | |||
| + | '''[[Дифференциалы элементарных функций]]''' — это дифференциалы от элементарных функций (табличные). | ||
| + | |||
| + | '''[[Дифференциалы сложных функций]]''' — это дифференциалы от функций, состоящих из внешней функции и внутренней функции (функция от функции). | ||
| + | |||
| + | '''Формулы дифференциалов сложных функций''' | ||
| + | |||
| + | [[файл:ДИФ04.JPG]] | ||
| + | [[файл:ДИФ04.png]] | ||
== Свойства дифференциалов == | == Свойства дифференциалов == | ||
| − | Для функций | + | Для функций '''u=f(x)''' и '''v=g(x)''' верны правила: |
| − | |||
[[файл:ДИФ03.png]] | [[файл:ДИФ03.png]] | ||
| − | При '''f(x)''' и | + | При '''f(x)''' и '''g(x)=C''' получаем: |
| − | |||
[[файл:ДИФ031.png]] | [[файл:ДИФ031.png]] | ||
| − | При '''f(x)=C''' и | + | При '''f(x)=C''' и '''g(x)''' получаем: |
| − | |||
[[файл:ДИФ032.png]] | [[файл:ДИФ032.png]] | ||
== Виды дифференциалов: == | == Виды дифференциалов: == | ||
{{Список Диф}} | {{Список Диф}} | ||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
| − | |||
= [[Математический анализ|Другие понятия:]] = | = [[Математический анализ|Другие понятия:]] = | ||
{{Список ДП}} | {{Список ДП}} | ||
Версия 07:08, 15 марта 2023
Дифференциал — это математический термин, обозначающий некое бесконечно малое приращение.
Содержание
Дифференциал функции
Определения
Дифференциал функции — это бесконечно малое приращение функции.
Дифференциал функции y=f(x) равен произведению производной функции на дифференциал аргумента.
Нахождение дифференциала функции называется дифференцированием, так как требует нахождения производной.
Дифференциалы элементарных функций — это дифференциалы от элементарных функций (табличные).
Дифференциалы сложных функций — это дифференциалы от функций, состоящих из внешней функции и внутренней функции (функция от функции).
Формулы дифференциалов сложных функций
Свойства дифференциалов
Для функций u=f(x) и v=g(x) верны правила:
При f(x) и g(x)=C получаем:
При f(x)=C и g(x) получаем:
Виды дифференциалов:
Другие понятия:
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara