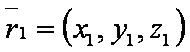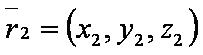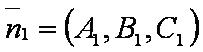Уравнение прямой, равноудалённой от трёх точек — различия между версиями
(начало) |
м |
||
| Строка 3: | Строка 3: | ||
Введём обозначения: | Введём обозначения: | ||
| − | [[файл: | + | [[файл:ВЕК79.JPG]] — радиус-[[вектор]] точки прямой; |
| − | [[файл: | + | [[файл:ВЕК71.JPG]] — радиус-вектор первой точки; |
| − | [[файл: | + | [[файл:ВЕК72.JPG]] — радиус-вектор второй точки; |
| − | [[файл: | + | [[файл:ВЕК73.JPG]] — радиус-вектор третьей точки; |
| − | [[файл: | + | [[файл:ВЕК91.JPG]] — нормаль к первой плоскости; |
| − | [[файл: | + | [[файл:ВЕК92.JPG]] — нормаль ко второй плоскости; |
[[файл:ПЛО01.JPG]] — уравнение первой плоскости; | [[файл:ПЛО01.JPG]] — уравнение первой плоскости; | ||
Версия 15:24, 8 февраля 2021
Будем считать, что прямая, равноудалённая от трёх точек, — это прямая, все точки которой одинаково удалены от заданных точек. Тогда эта прямая образуется пересечением двух плоскостей, равноудалённых от пар точек (при однозначном определении равноудалённой плоскости для двух точек).
Содержание
Обозначения
Введём обозначения:
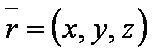
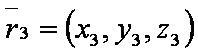
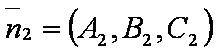
Формулы:
Векторная форма:
Координатная форма:
Другие уравнения:
- уравнение прямой, проходящей через две точки;
- уравнение прямой, равноудалённой от трёх точек;
- уравнение прямой, проходящей через точку в направлении вектора;
- уравнение прямой, проходящей через точку параллельно прямой;
- уравнение прямой, проходящей через точку перпендикулярно плоскости;
- уравнение прямой, образованной пересечением двух плоскостей;
- уравнение проекции прямой на плоскость;
- уравнение перпендикуляра из точки к прямой;
- уравнение перпендикуляра из точки к плоскости;
- уравнение перпендикуляра к двум прямым.