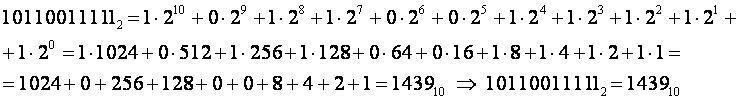Перевод чисел из двоичной системы счисления в четверичную
Перевод чисел из двоичной системы счисления в четверичную — это преобразование чисел двоичной системы счисления в числа четверичной системы счисления.
Содержание
- 1 Алгоритм
- 2 Пример перевода 2→4
- 3 Другие алгоритмы:
- 4 Ссылки
- 5 Примеры систем счисления:
- 6 Примеры алгоритмов:
- 6.1 Перевод чисел из десятичной системы счисления
- 6.2 Перевод чисел в десятичную систему счисления
- 6.3 Перевод чисел из двоичной системы счисления в четверичную
- 6.4 Перевод чисел из двоичной системы счисления в восьмеричную
- 6.5 Перевод чисел из двоичной системы счисления в шестнадцатеричную
- 6.6 Перевод чисел из четверичной системы счисления в двоичную
- 6.7 Перевод чисел из восьмеричной системы счисления в двоичную
- 6.8 Перевод чисел из шестнадцатеричной системы счисления в двоичную
- 7 Ссылки
Алгоритм
Исходное число двоичной системы счисления разбивается на пары цифр, начиная с цифры единиц (самой правой). Последняя (самая левая) пара может быть неполной, тогда в неё слева добавляется цифра 0. Затем пары цифр заменяются на соответствующие (по таблице пар) цифры четверичной системы счисления.
Таблица пар
- Заметим, что возможны другие способы перевода чисел: 2→8→4, 2→10→4 и 2→16→4.
Пример перевода 2→4
Другие алгоритмы:
- перевод чисел из двоичной системы счисления в четверичную;
- перевод чисел из двоичной системы счисления в восьмеричную;
- перевод чисел из двоичной системы счисления в шестнадцатеричную;
- перевод чисел из троичной системы счисления в девятеричную;
- перевод чисел из троичной системы счисления в девятеричную через десятичную;
- перевод чисел из четверичной системы счисления в двоичную;
- перевод чисел из четверичной системы счисления в восьмеричную;
- перевод чисел из четверичной системы счисления в восьмеричную через двоичную;
- перевод чисел из четверичной системы счисления в восьмеричную через десятичную;
- перевод чисел из четверичной системы счисления в шестнадцатеричную;
- перевод чисел из четверичной системы счисления в шестнадцатеричную через двоичную;
- перевод чисел из четверичной системы счисления в шестнадцатеричную через десятичную;
- перевод чисел из восьмеричной системы счисления в двоичную;
- перевод чисел из восьмеричной системы счисления в четверичную;
- перевод чисел из восьмеричной системы счисления в четверичную через двоичную;
- перевод чисел из восьмеричной системы счисления в четверичную через десятичную;
- перевод чисел из восьмеричной системы счисления в шестнадцатеричную через двоичную;
- перевод чисел из восьмеричной системы счисления в шестнадцатеричную через четверичную;
- перевод чисел из восьмеричной системы счисления в шестнадцатеричную через десятичную;
- перевод чисел из девятеричной системы счисления в троичную;
- перевод чисел из девятеричной системы счисления в троичную через десятичную;
- перевод чисел из шестнадцатеричной системы счисления в двоичную;
- перевод чисел из шестнадцатеричной системы счисления в четверичную;
- перевод чисел из шестнадцатеричной системы счисления в четверичную через двоичную;
- перевод чисел из шестнадцатеричной системы счисления в четверичную через десятичную;
- перевод чисел из шестнадцатеричной системы счисления в восьмеричную через двоичную;
- перевод чисел из шестнадцатеричной системы счисления в восьмеричную через четверичную;
- перевод чисел из шестнадцатеричной системы счисления в восьмеричную через десятичную;
- перевод чисел из десятичной системы счисления;
- перевод чисел в десятичную систему счисления;
- перевод чисел из одной системы счисления в другую через десятичную;
- перевод чисел из десятичной системы счисления в одиннадцатиричную специальную;
- перевод чисел из одиннадцатиричной специальной системы счисления в десятичную.
Ссылки
Система счисления — это система записи чисел с помощью цифр, причём положение цифры в числе определяет её вес и численное значение.
Система счисления полностью определяется основанием – числом, которое определяет число цифр (начиная с цифры ноль) в системе и степени которого (начиная с нулевой) определяют веса разрядов чисел (справа налево).
Примеры систем счисления:
- двоичная (цифры:0-1);
- троичная (цифры:0-2);
- четверичная (цифры:0-3);
- пятеричная (цифры:0-4);
- шестеричная (цифры:0-5);
- семеричная (цифры:0-6);
- восьмеричная (цифры:0-7);
- девятеричная (цифры:0-8);
- десятичная (цифры:0-9);
- одиннадцатеричная (цифры:0-9,A);
- двенадцатеричная (цифры:0-9,A-B);
- тринадцатеричная (цифры:0-9,A-C);
- четырнадцатеричная (цифры:0-9,A-D);
- пятнадцатеричная (цифры:0-9,A-E);
- шестнадцатеричная (цифры:0-9,A-F).
Для перевода чисел из одной системы счисления в другую используются алгоритмы перевода чисел.
Примеры алгоритмов:
Перевод чисел из десятичной системы счисления
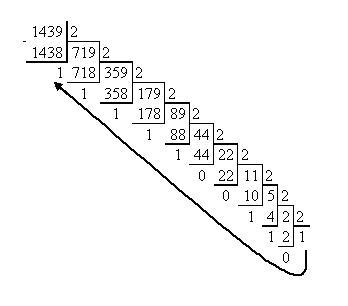
Сначала производится последовательное деление столбиком исходного числа и получаемых (от предыдущих делений) частных (больших или равных основанию) на основание новой системы счисления и записываются остатки от делений. Деление продолжается до тех пор, пока частное не станет меньше основания. Затем выписываются цифры в новой системе счисления вместо (полученных в десятичной системе счисления) последнего частного и остатков от делений в обратном (получению) порядке. Полученное число является записью исходного числа в новой системе счисления.
Пример перевода 10→2
143910=101100111112
Перевод чисел в десятичную систему счисления
Считается сумма произведений цифр исходной системы счисления (предварительно переведённых в десятичную систему счисления) на веса разрядов (основание системы счисления в степени номер разряда, начиная с нулевого) в исходной системе. Полученное число является записью исходного числа в десятичной системе счисления.
Пример перевода 2→10
Перевод чисел из двоичной системы счисления в четверичную
Исходное число двоичной системы счисления разбивается на пары цифр, начиная с цифры единиц (самой правой). Последняя (самая левая) пара может быть неполной, тогда в неё слева добавляется цифра 0. Затем пары цифр заменяются на соответствующие (по таблице пар) цифры четверичной системы счисления.
Таблица пар
Пример перевода 2→4
Перевод чисел из двоичной системы счисления в восьмеричную
Исходное число двоичной системы счисления разбивается на триады (тройки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) триада может быть неполной, тогда в неё слева добавляется цифра 0 (одна или две). Затем триады заменяются на соответствующие (по таблице триад) цифры восьмеричной системы счисления.
Таблица триад
Пример перевода 2→8
Перевод чисел из двоичной системы счисления в шестнадцатеричную
Исходное число двоичной системы счисления разбивается на тетрады (четвёрки цифр двоичной системы счисления), начиная с цифры единиц (самой правой). Последняя (самая левая) тетрада может быть неполной, тогда в неё слева добавляется цифра 0 (одна, две или три). Затем тетрады заменяются на соответствующие (по таблице тетрад) цифры шестнадцатеричной системы счисления.
Таблица тетрад
Пример перевода 2→16
Перевод чисел из четверичной системы счисления в двоичную
Цифры исходного числа четверичной системы счисления заменяются (слева направо) на соответствующие (по таблице пар) пары цифр двоичной системы счисления. Незначащий нуль первой (самой левой) пары опускается (отбрасывается).
Таблица пар
Пример перевода 4→2
Перевод чисел из восьмеричной системы счисления в двоичную
Цифры исходного числа восьмеричной системы счисления заменяются (слева направо) на соответствующие (по таблице триад) триады (тройки цифр двоичной системы счисления). Незначащие нули первой (самой левой) триады опускаются (отбрасываются).
Таблица триад
Пример перевода 8→2
Перевод чисел из шестнадцатеричной системы счисления в двоичную
Цифры исходного числа шестнадцатеричной системы счисления заменяются (слева направо) на соответствующие (по таблице тетрад) тетрады (четвёрки цифр двоичной системы счисления). Незначащие нули первой (самой левой) тетрады опускаются (отбрасываются).
Таблица тетрад
Пример перевода 16→2
