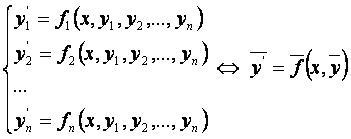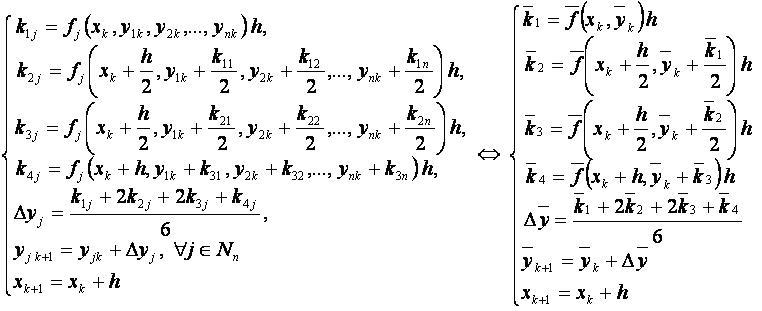Обобщённый метод Рунге-Кутты — различия между версиями
м |
|||
| Строка 1: | Строка 1: | ||
'''[[Классический метод Рунге-Кутты|Обобщённый метод Рунге-Кутты]]''' — это численный метод получения решения [[Матричная система дифференциальных уравнений динамического процесса|системы дифференциальных уравнений]]. Этот метод является обобщением [[классический метод Рунге-Кутты|классического метода Рунге-Кутты]] 4-го порядка для решения одного [[Линейное дифференциальное уравнение|дифференциального уравнения]]. | '''[[Классический метод Рунге-Кутты|Обобщённый метод Рунге-Кутты]]''' — это численный метод получения решения [[Матричная система дифференциальных уравнений динамического процесса|системы дифференциальных уравнений]]. Этот метод является обобщением [[классический метод Рунге-Кутты|классического метода Рунге-Кутты]] 4-го порядка для решения одного [[Линейное дифференциальное уравнение|дифференциального уравнения]]. | ||
| + | = Метод решения систем нелинейных уравнений = | ||
== Описание метода == | == Описание метода == | ||
Суть обобщённого метода Рунге-Кутты в пошаговом вычислении значений решения '''Y=Y(x)''' системы дифференциальных уравнений вида | Суть обобщённого метода Рунге-Кутты в пошаговом вычислении значений решения '''Y=Y(x)''' системы дифференциальных уравнений вида | ||
| Строка 15: | Строка 16: | ||
== Другие системы: == | == Другие системы: == | ||
{{Список СУ}} | {{Список СУ}} | ||
| − | == Ссылки | + | = [[Разделы математики|Другие разделы]] = |
| + | = Ссылки = | ||
*Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | *Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970. | ||
*[[Участник:Logic-samara]] | *[[Участник:Logic-samara]] | ||
[[Категория:Численные методы]] | [[Категория:Численные методы]] | ||
Версия 14:22, 28 января 2023
Обобщённый метод Рунге-Кутты — это численный метод получения решения системы дифференциальных уравнений. Этот метод является обобщением классического метода Рунге-Кутты 4-го порядка для решения одного дифференциального уравнения.
Содержание
Метод решения систем нелинейных уравнений
Описание метода
Суть обобщённого метода Рунге-Кутты в пошаговом вычислении значений решения Y=Y(x) системы дифференциальных уравнений вида
с начальным условием
Формулы
- Заметим, что обобщённый метод Рунге-Кутты является обобщением классического метода Рунге-Кутты, используемого для решения дифференциальных уравнений.
Другие методы:
- Для решения систем дифференциальных уравнений используется обобщённый метод Рунге-Кутты.
Другие системы:
Другие разделы
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.
- Участник:Logic-samara