Интегральный признак Коши — различия между версиями
| Строка 1: | Строка 1: | ||
| − | '''Интегральный признак Коши''' | + | '''Интегральный признак Коши''' — это признак сходимости для определения сходимости или расходимости '''[[ряд]]а''' [[файл:РЯД00.png]]. |
== Условие применимости == | == Условие применимости == | ||
Интегральный признак Коши применим для ряда [[файл:РЯД00.png]] при условии существования интегрируемой, непрерывной, положительной, монотонно убывающей в интервале '''[1,∞)''' функции '''f(x)''' такой, что [[файл:РЯД035.png]]. | Интегральный признак Коши применим для ряда [[файл:РЯД00.png]] при условии существования интегрируемой, непрерывной, положительной, монотонно убывающей в интервале '''[1,∞)''' функции '''f(x)''' такой, что [[файл:РЯД035.png]]. | ||
Текущая версия на 13:59, 23 марта 2023
Интегральный признак Коши — это признак сходимости для определения сходимости или расходимости ряда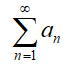 
.
Условие применимости
Интегральный признак Коши применим для ряда 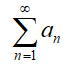при условии существования интегрируемой, непрерывной, положительной, монотонно убывающей в интервале [1,∞) функции f(x) такой, что 
.
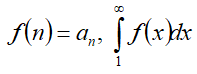Формулировка
Если несобственный интеграл 
сходится, то сходится и ряд .
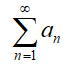Если несобственный интеграл расходится, то расходится и ряд .
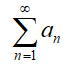Другие признаки:
Ссылки
- Кудрявцев В. А., Демидович Б. П. Краткий курс высшей математики. М.: «Наука», 1975.
- Участник:Logic-samara
