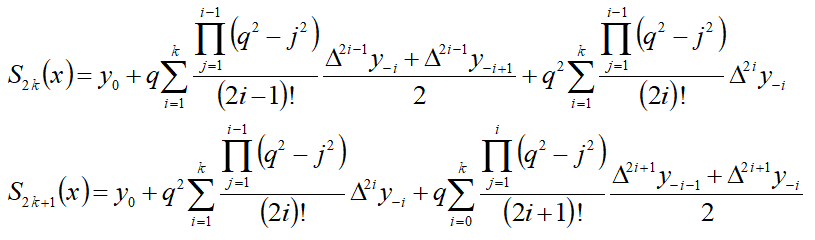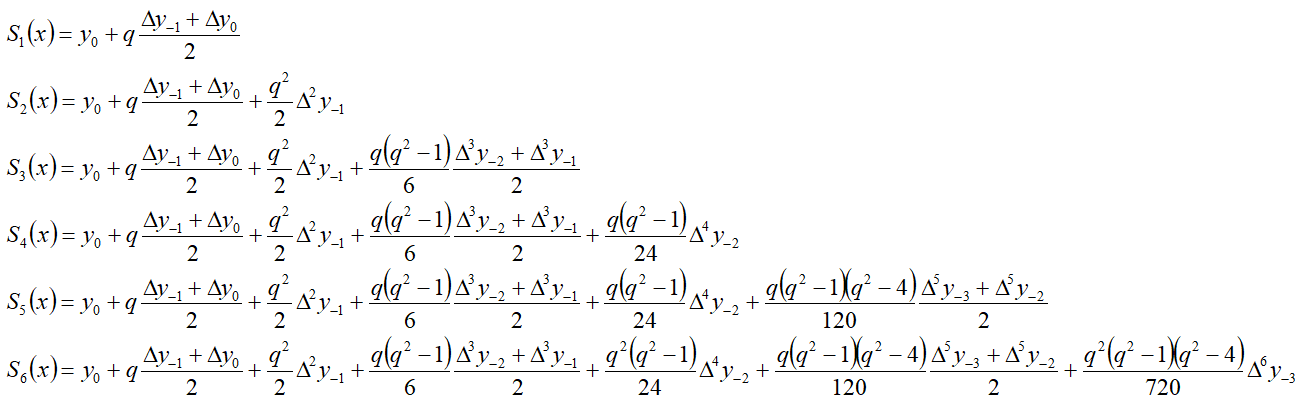Интерполяционная формула Стирлинга — различия между версиями
м |
м |
||
| (не показано 8 промежуточных версий этого же участника) | |||
| Строка 1: | Строка 1: | ||
'''Интерполяция Стирлинга''' — это определение значений многочлена '''n'''-ой степени (проходящего через заданные '''(2n+1)'''-у точку) в заданной точке по формуле. | '''Интерполяция Стирлинга''' — это определение значений многочлена '''n'''-ой степени (проходящего через заданные '''(2n+1)'''-у точку) в заданной точке по формуле. | ||
== Обозначения: == | == Обозначения: == | ||
| − | :<math>x</math> − заданная точка; | + | '''x''' − заданная точка; |
| + | |||
| + | '''S<sub>n</sub>(x)''' − значение формулы '''n'''-ого порядка в точке '''x'''; | ||
| + | |||
| + | '''(x<sub>j</sub>,y<sub>j</sub>)''' − точки (узлы) интерполяции '''(-n≤j≤n)'''; | ||
| + | |||
| + | '''h''' − шаг по оси абсцисс; | ||
| + | |||
| + | '''q=(x-x<sub>0</sub>)/h''' − параметр заданной точки '''(0<q≤0,25)'''; | ||
| + | |||
| + | '''x<sub>j</sub>= x<sub>0</sub>+jh''' − абсцисса '''j'''-той точки '''(-n≤j≤n)'''; | ||
| + | |||
| + | '''y<sub>j</sub>''' − ордината '''j'''-той точки '''(-n≤j≤n);''' | ||
| + | |||
| + | '''Δ<sup>1</sup>y<sub>j</sub>=y<sub>j+1</sub>-y<sub>j</sub>''' − '''j'''-ая конечная разность '''1'''-ого порядка '''(-n≤j≤n)'''; | ||
| + | |||
| + | '''Δ<sup>i</sup>y<sub>j</sub>=Δ<sup>i-1</sup><sub>j+1</sub>-Δ<sup>i-1</sup>y<sub>j</sub>''' − '''j'''-ая конечная разность '''i'''-ого порядка '''(i>1, -n≤j≤n)'''. | ||
| + | |||
| + | <!--:<math>x</math> − заданная точка; | ||
:<math>S_n(x)</math> − значение формулы n-ого порядка в точке x; | :<math>S_n(x)</math> − значение формулы n-ого порядка в точке x; | ||
:<math>(x_j,y_j)</math> − точки (узлы) интерполяции (-n≤j≤n); | :<math>(x_j,y_j)</math> − точки (узлы) интерполяции (-n≤j≤n); | ||
| Строка 9: | Строка 27: | ||
:<math>y_j</math> − ордината j-той точки (-n≤j≤n); | :<math>y_j</math> − ордината j-той точки (-n≤j≤n); | ||
:<math>\Delta^1y_j={y_{j+1}}-{y_j}</math> − j-ая конечная разность 1-ого порядка (-n≤j≤n); | :<math>\Delta^1y_j={y_{j+1}}-{y_j}</math> − j-ая конечная разность 1-ого порядка (-n≤j≤n); | ||
| − | :<math>\Delta^iy_j={\Delta^{i-1}y_{j+1}}-{\Delta^{i-1}y_j}</math> − j-ая конечная разность i-ого порядка (i>1, -n≤j≤n). | + | :<math>\Delta^iy_j={\Delta^{i-1}y_{j+1}}-{\Delta^{i-1}y_j}</math> − j-ая конечная разность i-ого порядка (i>1, -n≤j≤n).--> |
== Формула == | == Формула == | ||
[[файл:ИС00.png]] | [[файл:ИС00.png]] | ||
Текущая версия на 18:45, 25 октября 2024
Интерполяция Стирлинга — это определение значений многочлена n-ой степени (проходящего через заданные (2n+1)-у точку) в заданной точке по формуле.
Обозначения:
x − заданная точка;
Sn(x) − значение формулы n-ого порядка в точке x;
(xj,yj) − точки (узлы) интерполяции (-n≤j≤n);
h − шаг по оси абсцисс;
q=(x-x0)/h − параметр заданной точки (0<q≤0,25);
xj= x0+jh − абсцисса j-той точки (-n≤j≤n);
yj − ордината j-той точки (-n≤j≤n);
Δ1yj=yj+1-yj − j-ая конечная разность 1-ого порядка (-n≤j≤n);
Δiyj=Δi-1j+1-Δi-1yj − j-ая конечная разность i-ого порядка (i>1, -n≤j≤n).
Формула
- Интерполяционная формула Стирлинга является среднеарифметической первой и второй интерполяционных формул Гаусса.
Примеры формулы
Другие формулы:
- Линейная интерполяция;
- Интерполяция каноническим многочленом;
- Интерполяционная формула Бесселя;
- Интерполяционная формула Бесселя на середину;
- Интерполяционная формула Гаусса вперёд (первая формула);
- Интерполяционная формула Гаусса назад (вторая формула);
- Интерполяционная формула Лагранжа;
- Интерполяционная формула Ньютона вперёд (первая формула);
- Интерполяционная формула Ньютона назад (вторая формула);
- Интерполяционная формула Стирлинга.
Литература
- Ермаков В. И. Справочник по математике для экономистов — М.: Высшая школа, 1997, стр.312.