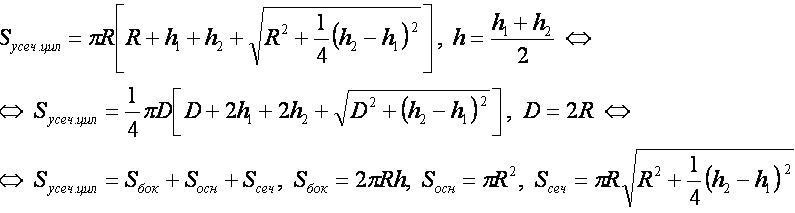Площадь поверхности усечённого цилиндра — различия между версиями
(начало) |
м |
||
| (не показаны 2 промежуточные версии этого же участника) | |||
| Строка 4: | Строка 4: | ||
Рассмотрим прямые круговые усечённые цилиндры без сечения основания. | Рассмотрим прямые круговые усечённые цилиндры без сечения основания. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''R''' — радиус основания цилиндра; | '''R''' — радиус основания цилиндра; | ||
| Строка 25: | Строка 23: | ||
== Формула == | == Формула == | ||
[[файл:ПУЦ01.JPG]] | [[файл:ПУЦ01.JPG]] | ||
| − | == Другие фигуры: == | + | == [[Площадь поверхности|Другие фигуры:]] == |
{{Список ПФВ}} | {{Список ПФВ}} | ||
== Ссылки == | == Ссылки == | ||
*Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.175. | *Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.175. | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 15:47, 18 февраля 2025
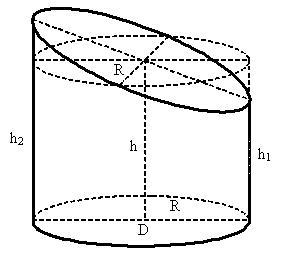
Площадь поверхности усечённого цилиндра — это сумма площадей основания, сечения и боковой поверхности усечённого цилиндра.
Рассмотрим прямые круговые усечённые цилиндры без сечения основания.
Содержание
Обозначения
R — радиус основания цилиндра;
D — диаметр основания цилиндра;
h — средняя высота усечённого цилиндра;
h1 — наименьшая высота усечённого цилиндра;
h2 — наибольшая высота усечённого цилиндра;
Sосн — площадь основания усечённого цилиндра;
Sсеч — площадь сечения усечённого цилиндра;
Sбок — площадь боковой поверхности усечённого цилиндра;
Sусеч.цил — площадь поверхности усечённого цилиндра.
Формула
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- шаровая бочка;
- круговая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.175.