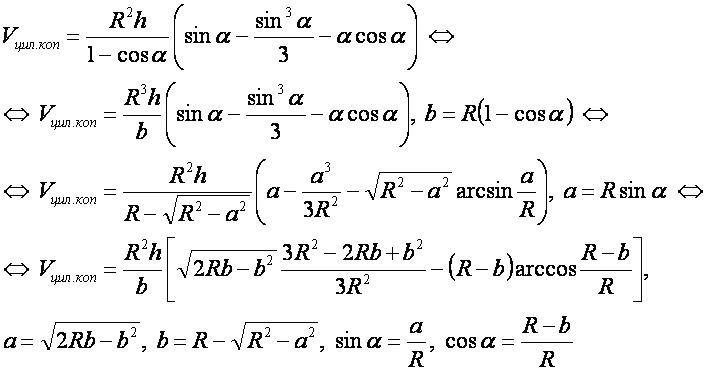Объём цилиндрического копыта — различия между версиями
(начало) |
м |
||
| (не показаны 3 промежуточные версии этого же участника) | |||
| Строка 28: | Строка 28: | ||
*Для вывода используется формула '''"[[объём трёхмерной фигуры]]"''' в прямоугольных координатах. | *Для вывода используется формула '''"[[объём трёхмерной фигуры]]"''' в прямоугольных координатах. | ||
*Заметим, что при '''α=π''' цилиндрическое копыто превращается в усечённый цилиндр с '''h<sub>1</sub>=0''' и '''h<sub>2</sub>=h''', а формула '''объёма цилиндрического копыта''' превращается в формулу '''[[Объём усечённого цилиндра|объёма усечённого цилиндра]]'''. | *Заметим, что при '''α=π''' цилиндрическое копыто превращается в усечённый цилиндр с '''h<sub>1</sub>=0''' и '''h<sub>2</sub>=h''', а формула '''объёма цилиндрического копыта''' превращается в формулу '''[[Объём усечённого цилиндра|объёма усечённого цилиндра]]'''. | ||
| − | == Другие фигуры: == | + | == [[Объём трёхмерной фигуры|Другие фигуры:]] == |
{{Список ОФВ}} | {{Список ОФВ}} | ||
== Ссылки == | == Ссылки == | ||
Текущая версия на 05:32, 11 февраля 2021
Объём цилиндрического копыта — это объём меньшей части цилиндра, ограниченной сечением цилиндра через основание и основанием.
Цилиндрическое копыто — это меньшая часть прямого кругового усечённого цилиндра с сечением одного основания. Цилиндрическое копыто иногда называют отрезком цилиндра.
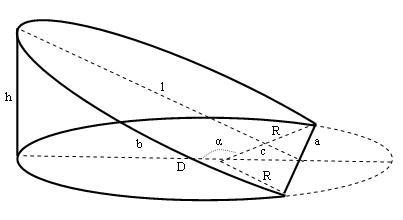
Обозначения
Введём обозначения:
R — радиус основания;
a — половина длины линии сечения основания;
b — высота основания;
c — расстояние от центра основания до линии сечения основания;
h — высота цилиндрического копыта;
l — высота сечения;
α — угол между радиусом основания, соединяющим центр основания и край линии сечения, и горизонтальной осью (проходящей через центры основания и линии сечения) ;
Vцил.коп — объём цилиндрического копыта.
Формула
Вывод формулы
- Для вывода используется формула "объём трёхмерной фигуры" в прямоугольных координатах.
- Заметим, что при α=π цилиндрическое копыто превращается в усечённый цилиндр с h1=0 и h2=h, а формула объёма цилиндрического копыта превращается в формулу объёма усечённого цилиндра.
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- параболоидное копыто;
- шаровая бочка;
- круговая бочка;
- параболическая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.175.
- Участник:Logic-samara