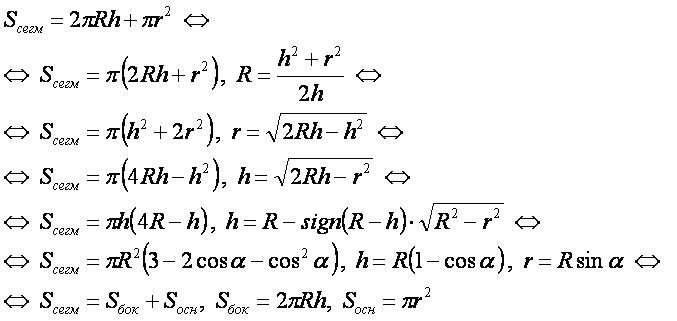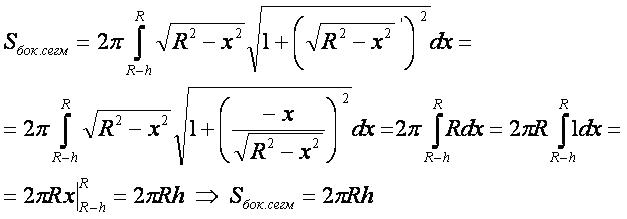Площадь поверхности шарового сегмента — различия между версиями
(начало) |
м |
||
| (не показана 1 промежуточная версия этого же участника) | |||
| Строка 20: | Строка 20: | ||
[[файл:ПСГ02.JPG]] | [[файл:ПСГ02.JPG]] | ||
*Для вывода используется формула 1 '''"[[площадь поверхности фигуры вращения]]"'''. | *Для вывода используется формула 1 '''"[[площадь поверхности фигуры вращения]]"'''. | ||
| − | == Другие фигуры: == | + | == [[Площадь поверхности|Другие фигуры:]] == |
{{Список ПФВ}} | {{Список ПФВ}} | ||
== Ссылки == | == Ссылки == | ||
Текущая версия на 05:41, 11 февраля 2021
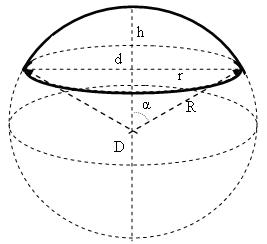
Площадь поверхности шарового сегмента — это сумма боковой площади шарового сегмента и площади основания сегмента.
Обозначения
Введём обозначения:
R — радиус шара;
r — радиус основания шарового сегмента;
h — высота шарового сегмента;
Sосн — площадь основания шарового сегмента;
Sбок — площадь боковой поверхности шарового сегмента;
Sсегм — площадь поверхности шарового сегмента.
Формула
Вывод формулы
- Для вывода используется формула 1 "площадь поверхности фигуры вращения".
Другие фигуры:
- фигура вращения;
- шар;
- цилиндр;
- конус;
- усечённый цилиндр;
- усечённый конус;
- шаровой сегмент;
- шаровой сектор;
- шаровой слой;
- шаровой клин;
- центральный шаровой клин;
- торовый клин;
- цилиндрическая труба;
- цилиндрическое копыто;
- конусное копыто;
- шаровое копыто;
- шаровая бочка;
- круговая бочка;
- сегментное кольцо;
- тор;
- кокон;
- купол;
- сфероид;
- параболоид.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.177.
- Участник:Logic-samara