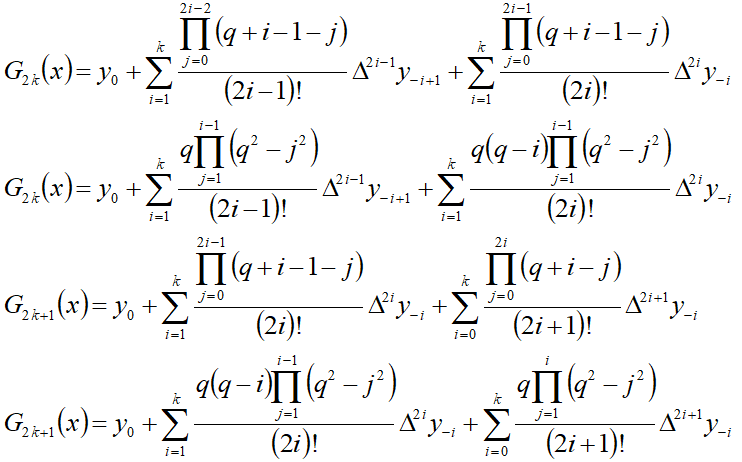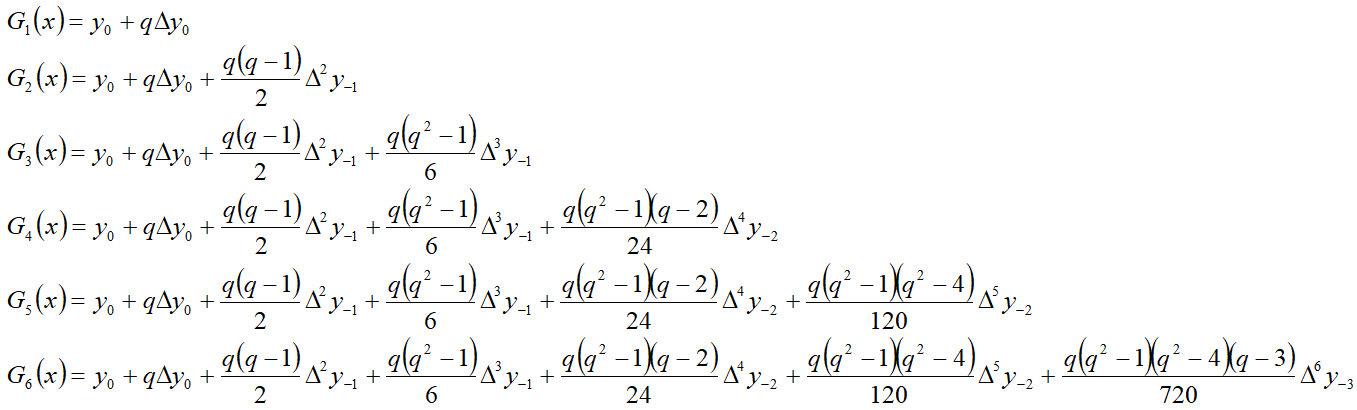Интерполяционная формула Гаусса вперёд — различия между версиями
(начало) |
м |
||
| Строка 20: | Строка 20: | ||
:<math>G_{2k+1}(x)=y_0+\sum\limits_{i=1}^k{\frac{q\left(q-i\right)\prod\limits_{j=1}^{i-1}{\left(q^2-j^2\right)}}{\left(2i\right)!}\Delta^{2i}y_{-i}}+\sum\limits_{i=0}^k{\frac{q\prod\limits_{j=1}^i{\left(q^2-j^2\right)}}{\left(2i+1\right)!}\Delta^{2i+1}y_{-i}},q=\frac{x-x_0}{h}</math>--> | :<math>G_{2k+1}(x)=y_0+\sum\limits_{i=1}^k{\frac{q\left(q-i\right)\prod\limits_{j=1}^{i-1}{\left(q^2-j^2\right)}}{\left(2i\right)!}\Delta^{2i}y_{-i}}+\sum\limits_{i=0}^k{\frac{q\prod\limits_{j=1}^i{\left(q^2-j^2\right)}}{\left(2i+1\right)!}\Delta^{2i+1}y_{-i}},q=\frac{x-x_0}{h}</math>--> | ||
== Примеры формулы == | == Примеры формулы == | ||
| − | <!--:<math>q=\frac{x-x_0}{h}</math> | + | <!--:<math>q=\frac{x-x_0}{h}</math>--> |
[[файл:ИГ11.png]] | [[файл:ИГ11.png]] | ||
| − | === Линейная интерполяция (n=1) === | + | <!--=== Линейная интерполяция (n=1) === |
| − | + | :<math>G_1(x)=y_0+q\Delta y_0</math> | |
=== Квадратическая интерполяция (n=2) === | === Квадратическая интерполяция (n=2) === | ||
| − | <!--:<math>G_2(x)=y_0+q\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}</math | + | <!--:<math>G_2(x)=y_0+q\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}</math> |
=== Кубическая интерполяция (n=3) === | === Кубическая интерполяция (n=3) === | ||
| − | + | :<math>G_3(x)=y_0+\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}+\frac{q\left(q^2-1\right)}{6}\Delta^3 y_{-1}</math> | |
=== Интерполяция многочленом 4-й степени (n=4) === | === Интерполяция многочленом 4-й степени (n=4) === | ||
| − | + | :<math>G_4(x)=y_0+\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}+\frac{q\left(q^2-1\right)}{6}\Delta^3 y_{-1}+\frac{q^2\left(q^2-1\right)\left(q-2\right)}{24}\Delta^4 y_{-2}</math> | |
=== Интерполяция многочленом 5-й степени (n=5) === | === Интерполяция многочленом 5-й степени (n=5) === | ||
| − | + | :<math>G_5(x)=y_0+\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}+\frac{q\left(q^2-1\right)}{6}\Delta^3 y_{-1}+\frac{q^2\left(q^2-1\right)\left(q-2\right)}{24}\Delta^4 y_{-2}+\frac{q\left(q^2-1\right)\left(q^2-4\right)}{120}\Delta^5 y_{-2}</math> | |
=== Интерполяция многочленом 6-й степени (n=6) === | === Интерполяция многочленом 6-й степени (n=6) === | ||
| − | + | :<math>G_6(x)=y_0+\Delta y_0+\frac{q\left(q-1\right)}{2}\Delta^2 y_{-1}+\frac{q\left(q^2-1\right)}{6}\Delta^3 y_{-1}+\frac{q^2\left(q^2-1\right)\left(q-2\right)}{24}\Delta^4 y_{-2}+\frac{q\left(q^2-1\right)\left(q^2-4\right)}{120}\Delta^5 y_{-2}+\frac{q^2\left(q^2-1\right)\left(q^2-4\right)\left(q-3\right)}{720}\Delta^6 y_{-3}</math>--> | |
== [[Интерполяция|Другие формулы:]] == | == [[Интерполяция|Другие формулы:]] == | ||
{{Список МИН}} | {{Список МИН}} | ||
Версия 18:19, 25 октября 2024
Интерполяция Гаусса вперёд (первая формула) — это определение значений многочлена n-ой степени (проходящего через заданные (2n+1)-у точку) в заданной точке по формуле.
Обозначения:
- <math>x</math> − заданная точка;
- <math>G_{n}(x)</math> − значение формулы n-ого порядка в точке x;
- <math>(x_j,y_j)</math> − точки (узлы) интерполяции (-n≤j≤n);
- <math>h</math> − шаг по оси абсцисс;
- <math>q=\frac{x-x_0}{h}</math> − параметр заданной точки (q>0);
- <math>x_j= x_0 + jh</math> − абсцисса j-той точки (-n≤j≤n);
- <math>y_j</math> − ордината j-той точки (-n≤j≤n);
- <math>\Delta^1y_j={y_{j+1}}-{y_j}</math> − j-ая конечная разность 1-ого порядка (-n≤j≤n);
- <math>\Delta^iy_j={\Delta^{i-1}y_{j+1}}-{\Delta^{i-1}y_j}</math> − j-ая конечная разность i-ого порядка (i>1, -n≤j≤n).
Формула
Примеры формулы
Другие формулы:
- Линейная интерполяция;
- Интерполяция каноническим многочленом;
- Интерполяционная формула Бесселя;
- Интерполяционная формула Бесселя на середину;
- Интерполяционная формула Гаусса вперёд (первая формула);
- Интерполяционная формула Гаусса назад (вторая формула);
- Интерполяционная формула Лагранжа;
- Интерполяционная формула Ньютона вперёд (первая формула);
- Интерполяционная формула Ньютона назад (вторая формула);
- Интерполяционная формула Стирлинга.