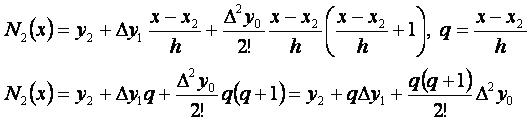Интерполяционная формула Ньютона назад — различия между версиями
м |
м |
||
| Строка 21: | Строка 21: | ||
== Ссылки == | == Ссылки == | ||
*Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970. | *Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970. | ||
| − | |||
[[Категория:Математика]][[Категория:Численные методы]] | [[Категория:Математика]][[Категория:Численные методы]] | ||
Версия 17:52, 25 октября 2024
Интерполяция Ньютона назад — это определение значений многочлена n-ой степени (проходящего через заданные (n+1)-у точку) в заданной точке по формуле с помощью приращений назад.
Формула
Преимущество второй интерполяционной формулы Ньютона по сравнению с формулой Лагранжа состоит в том, что при изменении степени n у интерполяционного многочлена Ньютона требуется только добавить или отбросить соответствующее число стандартных слагаемых (это удобно на практике), тогда как интерполяционный многочлен Лагранжа требуется строить заново. На практике применение второй интерполяционной формулы Ньютона удобнее для равноотстоящих узлов или узлов с равными промежутками.
При n=1 вторая формула Ньютона имеет вид:
При n=2 вторая формула Ньютона имеет вид:
При n=3 вторая формула Ньютона имеет вид:
Другие формулы:
- Линейная интерполяция;
- Интерполяция каноническим многочленом;
- Интерполяционная формула Бесселя;
- Интерполяционная формула Бесселя на середину;
- Интерполяционная формула Гаусса вперёд (первая формула);
- Интерполяционная формула Гаусса назад (вторая формула);
- Интерполяционная формула Лагранжа;
- Интерполяционная формула Ньютона вперёд (первая формула);
- Интерполяционная формула Ньютона назад (вторая формула);
- Интерполяционная формула Стирлинга.
Ссылки
- Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970.