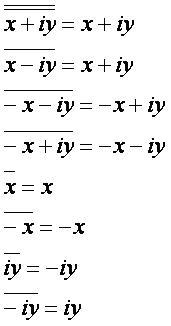Комплексно сопряжённые числа — различия между версиями
(начало) |
м |
||
| Строка 1: | Строка 1: | ||
'''Комплексно сопряжёнными числами''' называются [[комплексные числа]] с равными [[Действительные числа|действительными]] частями и противоположными мнимыми частями. | '''Комплексно сопряжёнными числами''' называются [[комплексные числа]] с равными [[Действительные числа|действительными]] частями и противоположными мнимыми частями. | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''x''' — действительная часть (абсцисса) комплексно сопряжённых чисел; | '''x''' — действительная часть (абсцисса) комплексно сопряжённых чисел; | ||
| Строка 27: | Строка 25: | ||
{{Список Чис}} | {{Список Чис}} | ||
== Ссылки == | == Ссылки == | ||
| − | |||
[[Категория:Математика]][[Категория:Числа]] | [[Категория:Математика]][[Категория:Числа]] | ||
Текущая версия на 15:03, 18 февраля 2025
Комплексно сопряжёнными числами называются комплексные числа с равными действительными частями и противоположными мнимыми частями.
Обозначения
x — действительная часть (абсцисса) комплексно сопряжённых чисел;
y — мнимая часть (ордината) первого числа;
-y — мнимая часть (ордината) второго числа;
r — модуль комплексно сопряжённых чисел;
φ — аргумент первого числа;
-φ — аргумент второго числа;
x+iy — первое комплексно сопряжённое число;
x-iy — второе комплексно сопряжённое число.
Формулы:
Примеры:
Другие операции:
- сложение чисел;
- вычитание чисел;
- умножение чисел;
- деление чисел;
- обращение числа;
- возведение в степень;
- извлечение квадратного корня;
- извлечение кубического корня;
- извлечение корня n-ой степени;
- логарифмирование числа;
- возведение в комплексную степень;
- тригонометрические функции комплексных чисел;
- гиперболические функции комплексных чисел;
- взятие комплексно сопряжённого числа;