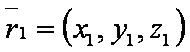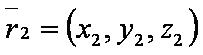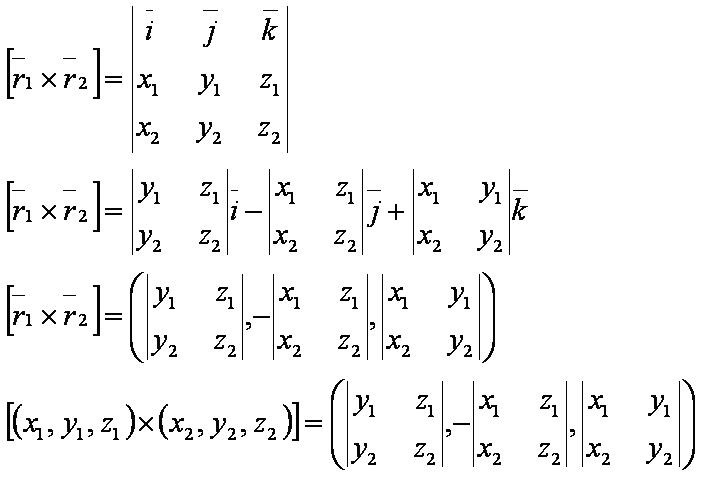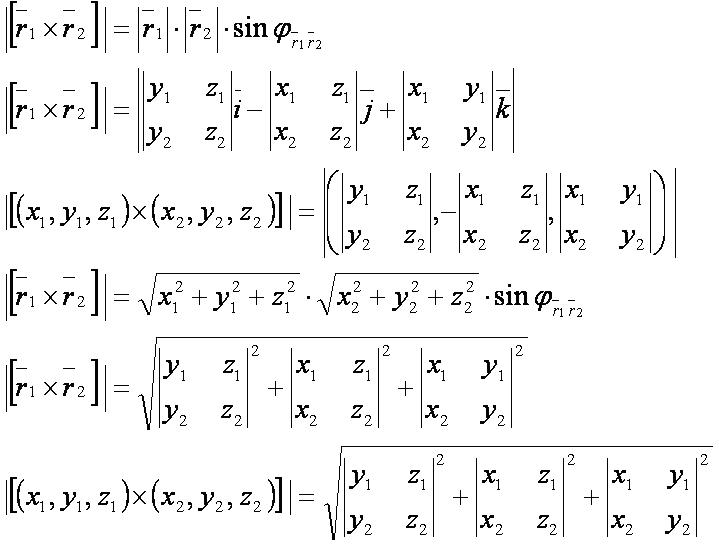Векторное произведение
Версия от 15:17, 23 октября 2024; Logic-samara (обсуждение | вклад)
Векторное произведение двух векторов - это вектор, перпендикулярный векторам-сомножителям, причём перемножаемые векторы и вектор произведения образуют правую тройку векторов.
Геометрический смысл модуля векторного произведения векторов - это величина площади параллелограмма, построенного на этих векторах.
Содержание
Обозначения
Формула
Свойства
Модуль векторного произведения выражается формулой:
- Заметим, что в формулах 0<φr1r2<π.
Другие операции:
- нахождение длины вектора;
- умножение вектора на число;
- возведение в квадрат координат вектора;
- извлечение корня из координат вектора;
- сложение векторов;
- вычитание векторов;
- умножение координат векторов;
- деление координат векторов;
- скалярное произведение;
- векторное произведение;
- смешанное произведение;
- двойное векторное произведение;
- нахождение угла между векторами;
- ортогонализация векторов.
Ссылки
- Корн Г., Корн Т. Справочник по математике для научных работников и инженеров. М.: Наука, 1970.