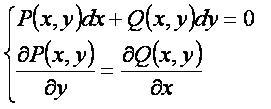Уравнение в полных дифференциалах

Уравнения в полных дифференциалах — это уравнения, в которых левая часть является полным дифференциалом некоторой функции F(x,y) а правая равна нулю.

Будем рассматривать уравнения первого порядка в полных дифференциалах вида P(x,y)dx+Q(x,y)dy=0.

В том случае, когда функции P(x,y) и Q(x,y) и их частные производные непрерывны в односвязной области, уравнение P(x,y)dx+Q(x,y)dy=0 будет уравнением в полных дифференциалах, если ∂P(x,y)/∂y=∂Q(x,y)/∂x.

Обозначения

Введём обозначения:

x – переменная - аргумент функции;

y – переменная – функция;

dx – дифференциал аргумента;

dy – дифференциал функции;

F(x,y) – первообразная функция, при равенстве константе задающая неявно решение y=y(x).

Уравнение

Общее решение

Другие дифференциальные уравнения:

• с разделяющимися переменными;
• однородное;
• линейное;
• уравнение Бернулли;
• уравнение в полных дифференциалах;
• уравнение Клеро;
• уравнение второго порядка, не содержащее y и y^’;
• уравнение второго порядка, не содержащее y;
• уравнение второго порядка, не содержащее x;
• однородное уравнение второго порядка с постоянными коэффициентами;
• неоднородное уравнение второго порядка с постоянными коэффициентами;
• уравнение n-ого порядка, содержащее только переменную x;
• однородное уравнение n-ого порядка с постоянными коэффициентами;
• неоднородное уравнение n-ого порядка с постоянными коэффициентами;
• общее дифференциальное уравнение.

Ссылки

• Бермант А.Ф., Араманович И.Г. Краткий курс математического анализа для втузов. М.: Наука, 1973, стр.540.
• Участник:Logic-samara