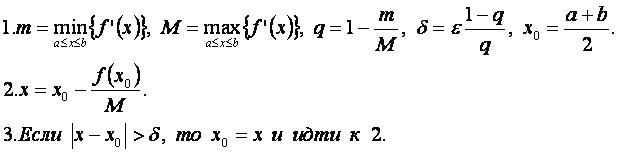Универсальный метод итераций
Универсальный метод итераций — это численный метод нахождения (одного) решения (с заданной точностью ε) нелинейного уравнения вида f(x)=0.
Описание метода
Суть универсального метода итераций состоит в расчётах новой точки x (итерациях) по формуле x=x-f(x)/M, которая похожа на формулы метода итераций и метода касательных и строится с помощью функции f(x), где M=max{f’(x)}.
Итерации продолжаются до достижения необходимой точности решения ε.
Универсальный метод итераций строит зависимость вида x=φ(x) (как в методе итераций), но не из уравнения f(x)=0, а по универсальной формуле x=x-f(x)/M (как в методе касательных), т.е. φ(x)=x-f(x)/M.
Универсальный метод итераций применим, если функция f(x) непрерывна и дифференцируема на отрезке [a,b], а функция f’(x) на отрезке [a,b] везде положительна (0<f’(x)<∞).
Если же функция f’(x) на отрезке [a,b] везде отрицательна (-∞<f’(x)<0), то универсальный метод итераций применим для решения уравнения вида -f(x)=0 (очевидно, что уравнение -f(x)=0 эквивалентно уравнению f(x)=0).
Для решения используются вспомогательные параметры m, M, q и δ, где δ - уточнённая точность. M=max{f’(x)}, m=min{f’(x)}.
Очевидно, что q=max|φ’(x)|=max|1-f’(x)/M|=1-m/M<1, т.е. для функции φ(x)=x-f(x)/M выполняются требования метода итераций.
Сначала находим отрезок [a,b] такой, что функция f(x) непрерывна, дифференцируема и меняет знак на отрезке, т.е. f(a)f(b)<0.
Далее применяем алгоритм решения.
Алгоритм решения
Входные данные: f(x), f’(x), a, b, ε.
Выходные данные: x.
Значение x является решением с заданной точностью ε нелинейного уравнения вида f(x)=0.
Если f(x)=0, то x - точное решение.
Другие методы:
- Для решения систем нелинейных уравнений используется метод Ньютона.
Ссылки
- Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970.
- Участник:Logic-samara
