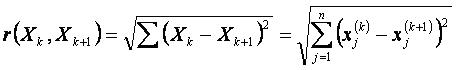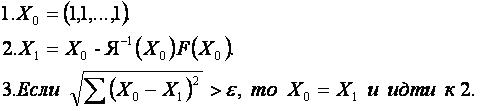Метод Ньютона

Метод Ньютона — это численный метод решения системы нелинейных уравнений вида F(X)=0 с заданной точностью ε.

Методы решения системы нелинейных уравнений

Описание метода

Суть метода Ньютона состоит в расчётах новой точки X по старой точке.

Для решения методом Ньютона системы n нелинейных уравнений с n неизвестными, то есть системы вида:

где f_i(x₁,x₂,… ,x_n) для 1≤i≤n, дважды непрерывно дифференцируема (в некоторой окрестности решения X системы уравнений F(X)=0), сначала находим матрицу из частных производных для системы функций f₁(x₁,x₂,… ,x_n), f₂(x₁,x₂,… ,x_n), …, f_n(x₁,x₂,… ,x_n), которая называется матрицей Якоби:

Затем для k=0 выбираем начальную точку X₀ в некоторой окрестности решения X*, причём ΔЯ(X₀)≠0, например X₀=(1;1;…;1). Далее на (k+1)-шаге вычисляем матрицу Якоби Я(X_k)=F’(X_k), систему функций F(X_k) в точке X_k, и новую точку X_k+1 вычисляем по формуле:

Расстояние между точками определяется по формуле:

Итерации продолжаются до достижения необходимой точности решения ε.

Алгоритм решения

Входные данные: F, Я, ε.

Выходные данные: X₁.

• Заметим, что метод Ньютона при n=1, то есть для нелинейного уравнения f₁(x₁)=0, становится методом касательных.

Другие методы:

• метод Крамера;
• метод обратной матрицы;
• метод неполного решения;
• метод Гаусса;
• метод простых итераций;
• метод Зейделя.

• Для решения систем нелинейных уравнений используется метод Ньютона.

Другие системы:

• система линейных уравнений;
• система нелинейных уравнений;
• векторная система дифференциальных уравнений;
• матричная система дифференциальных уравнений;
• система дифференциальных уравнений;
• система управления запасами;
• система массового обслуживания.

Ссылки

• Демидович Б. П., Марон И. А. Основы вычислительной математики. М.: Наука, 1970.
• Участник:Logic-samara