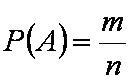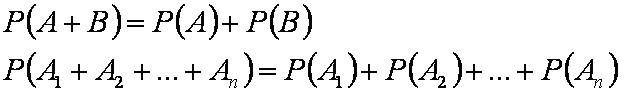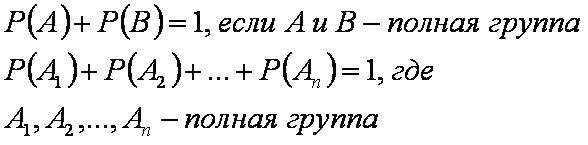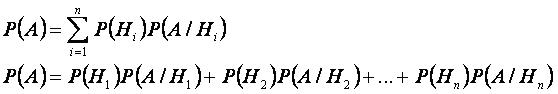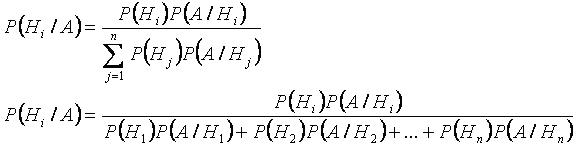Вероятность

Вероятность — это количественная мера возможности появления события.

Вероятность

Определения

Случай называется благоприятствующим данному событию, если появление его влечёт за собой появление этого события.

Вероятность события — это число, равное отношению числа благоприятствующих случаев к общему числу равновозможных случаев.

Формулы:

, где

P(A) — вероятность события;

m — число благоприятствующих событию A случаев;

n — общее число равновозможных случаев.

Для вероятности верно неравенство:

События называются несовместными, если они не могут наблюдаться в одном и том же испытании одновременно.

Суммой нескольких событий называется событие, состоящее в появлении хотя бы одного из этих событий.

Формула вероятности суммы несовместных событий

Вероятность суммы несовместных событий равна сумме вероятностей этих событий:

Если в единичном опыте обязательно должно произойти одно из событий, то такая группа событий называется полной группой событий. Сумма вероятностей несовместных событий, образующих полную группу, равна единице:

События называются независимыми, если появление одного из событий не меняет вероятности появления другого.

Произведением нескольких событий называется событие, состоящее в одновременном появлении всех этих событий.

Формула вероятности произведения независимых событий

Вероятность произведения независимых событий равна произведению вероятностей каждого события:

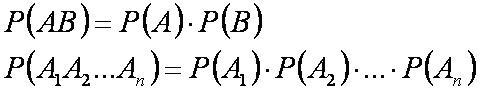
Для зависимых событий вероятности появления одних событий зависят от того, произошло другое событие или нет.

Вероятность события A, вычисленная при условии, что имело место другое событие B, называется условной вероятностью события A и обозначается P(A/B).

Вероятность события A₁, вычисленная при условии, что имели место события A₂,A₃,...,A_n, называется условной вероятностью события A₁ и обозначается P(A₁/ A₂,A₃,...,A_n).

Формула вероятности произведения двух событий

Вероятность произведения двух событий равна произведению вероятности одного из них на условную вероятность другого, вычисленную при условии, что первое событие имело место:

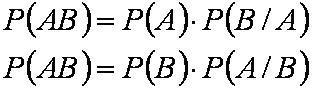
Формула вероятности суммы двух событий

Сумма вероятностей двух событий равна сумме вероятностей этих событий за вычетом вероятности произведения этих событий:

Формула условной вероятности

Условная вероятность одного события (при условии, что другое событие имело место) равна отношению вероятности произведения двух событий к вероятности другого события:

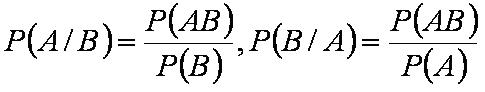
Формула полной вероятности

Формула Байеса

• Формула Байеса позволяет «переставить причину и следствие»: по известному факту события вычислить вероятность того, что оно было вызвано данной причиной. События, отражающие действие «причин», в данном случае называют гипотезами, так как они — предполагаемые события, повлёкшие данное. Безусловную вероятность справедливости гипотезы называют априорной (насколько вероятна причина вообще), а условную — с учётом факта произошедшего события — апостериорной (насколько вероятна причина оказалась с учётом данных о событии)(формулировка из Википедии).

Другие разделы:

• Теория вероятностей:
  • вероятность;
  • распределения вероятностей;
  • локальная теорема Лапласа;
  • интегральная теорема Лапласа;
  • диаграмма Венна;
  • диаграмма Эйлера;
• Математическая статистика:
  • дискретная случайная величина;
  • непрерывная случайная величина;
  • интервальный ряд;
  • гипотезы;
  • доверительные интервалы;
• Статистика:
  • коэффициенты;
• Экономическая статистика:
  • индексы;
  • показатели динамики;
• Случайные процессы:
  • система управления запасами;
  • система массового обслуживания;
• Логистика:
  • логистические алгоритмы;
  • транспортные задачи;
• Теория игр:
  • игра;
  • критерии.

Ссылки

• Справочник по математике для экономистов. Под ред. проф. В.И.Ермакова. М.: Высшая школа, 1987.
• Участник:Logic-samara