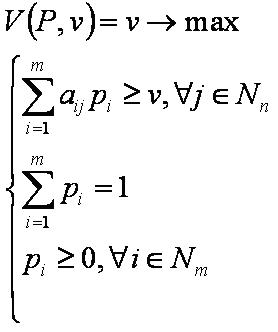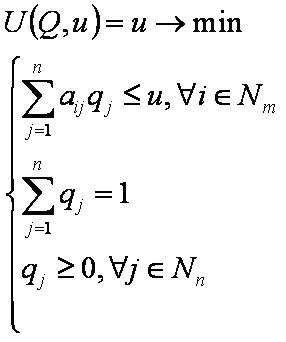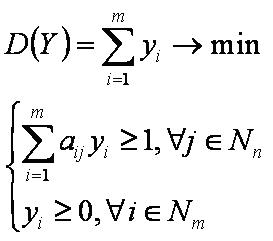Матричная игра

Математическая модель МИ1

Математическая модель МИ2

Матричная игра — это задача теории игр — парная игра с нулевой суммой, в которой каждый игрок имеет конечное число чистых стратегий.

Матричные игры

Определения

Игра называется парной, если в ней сталкиваются интересы двух противников.

Игра называется с нулевой суммой, если один игрок выигрывает столько, сколько второй проигрывает в той же партии.

Каждая фиксированная стратегия, которую может выбрать игрок, называется его чистой стратегией.

Смешанной стратегией игрока называется набор чистых стратегий, задаваемый вероятностями (относительными частотами) выбора соответствующих чистых стратегий.

Постановка задачи

Введём обозначения:

m — число стратегий первого игрока;

n — число стратегий второго игрока.

a_ij — элемент платёжной матрицы A – выигрыш первого игрока (соответственно, проигрыш второго игрока), если первый игрок выберет i-ую стратегию, а второй игрок – j-ую стратегию;

p_i — вероятность (относительная частота) выбора первым игроком i-ой стратегии;

q_j — вероятность (относительная частота) выбора вторым игроком – j-ой стратегии;

P=(p₁, p₂, …, p_m) — смешанная стратегия первого игрока;

Q=(q₁, q₂, …, q_n) — смешанная стратегия второго игрока;

V(P,v)=v — выигрыш первого игрока;

U(Q,u)=u — проигрыш второго игрока.

Задача первого игрока

Задача первого игрока выбрать смешанную стратегию максимизирующую выигрыш.

Задача второго игрока

Задача второго игрока выбрать смешанную стратегию минимизирующую проигрыш.

Эквивалентная задача

Введём обозначения:

D(Y)=1/v — обратная величина выигрыша первого игрока;

L(X)=1/u — обратная величина проигрыша второго игрока.

y_i=p_i/v — относительная величина выбора первым игроком i-ой стратегии;

x_j=q_j/u — относительная величина выбора вторым игроком j-ой стратегии.

Эквивалентная задача первого игрока

Задача первого игрока минимизировать обратную величину своего выигрыша.

Эквивалентная задача второго игрока

Задача второго игрока максимизировать обратную величину своего проигрыша.

Эквивалентные задачи являются парой двойственных задач линейного программирования.

Другие разделы:

• Теория вероятностей:
  • вероятность;
  • распределения вероятностей;
  • локальная теорема Лапласа;
  • интегральная теорема Лапласа;
  • диаграмма Венна;
  • диаграмма Эйлера;
• Математическая статистика:
  • дискретная случайная величина;
  • непрерывная случайная величина;
  • интервальный ряд;
  • гипотезы;
  • доверительные интервалы;
• Статистика:
  • коэффициенты;
• Экономическая статистика:
  • индексы;
  • показатели динамики;
• Случайные процессы:
  • система управления запасами;
  • система массового обслуживания;
• Логистика:
  • логистические алгоритмы;
  • транспортные задачи;
• Теория игр:
  • игра;
  • критерии.

Ссылки

• Справочник по математике для экономистов. Под ред. проф. В.И.Ермакова. М.: Высшая школа, 1987, стр.245.
• Участник:Logic-samara