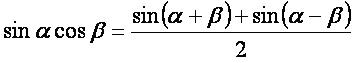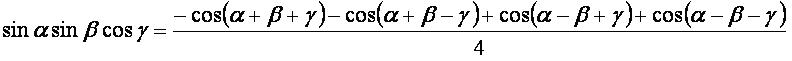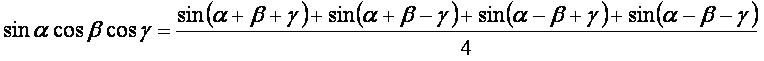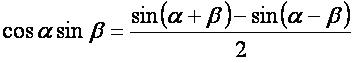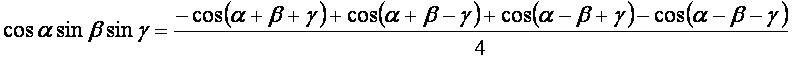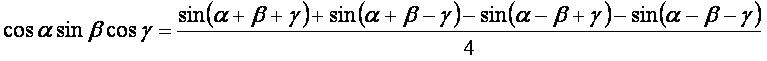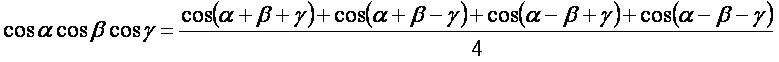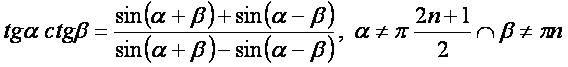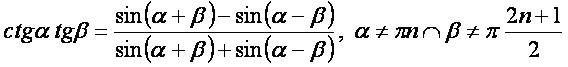Произведение тригонометрических функций

Произведение тригонометрических функций — это произведение, в котором сомножители являются тригонометрическими функциями.

Формулы:

sinα:

sinα·sinβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

sinα·cosβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

sinα·sinβ·sinγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

sinα·sinβ·cosγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

sinα·cosβ·sinγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

sinα·cosβ·cosγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα:

cosα·sinβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα·cosβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα·sinβ·sinγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα·sinβ·cosγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα·cosβ·sinγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

cosα·cosβ·cosγ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

tgα:

tgα·tgβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

tgα·ctgβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

ctgα:

ctgα·tgβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

ctgα·ctgβ:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

Другие формулы:

• тригонометрические функции углов;
• сумма тригонометрических функций;
• разность тригонометрических функций;
• произведение тригонометрических функций;
• тригонометрические функции суммы углов;
• тригонометрические функции разности углов;
• тригонометрические формулы приведения;
• тригонометрические функции кратных углов;
• тригонометрические функции половинного угла;
• тригонометрические функции угла, полученного многократным делением пи на два;
• выражение тригонометрических функций через другую;
• выражение тригонометрических функций через гиперболические;
• тригонометрические функции комплексной переменной;
• производные тригонометрических функций;
• дифференциалы тригонометрических функций;
• интегралы тригонометрических функций;
• графики тригонометрических функций.

Ссылки

• Бронштейн М. Н., Семендяев К. А., Справочник по математике. М., 1956, стр.184.
• Участник:Logic-samara