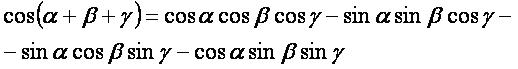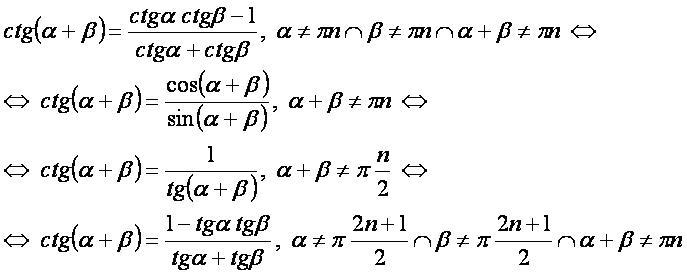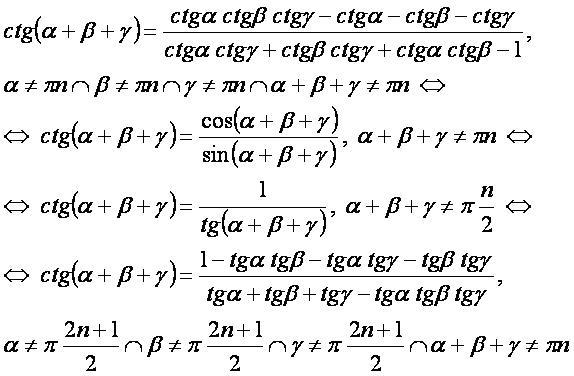Тригонометрические функции суммы углов

Тригонометрические функции суммы углов — это тригонометрические функции, в которых аргументами являются суммы углов.

Формулы:

sin(α+β):

sin(α+β+γ):

cos(α+β):

cos(α+β+γ):

tg(α+β):

• Заметим, что последняя формула получается из первой умножением числителя и знаменателя на произведение котангенсов двух углов.

tg(α+β+γ):

• Заметим, что последняя формула получается из первой умножением числителя и знаменателя на произведение котангенсов трёх углов.

ctg(α+β):

• Заметим, что все формулы для котангенса суммы двух углов получаются обращением соответствующих дробей в формулах тангенса.

ctg(α+β+γ):

• Заметим, что все формулы для котангенса суммы трёх углов получаются обращением соответствующих дробей в формулах тангенса.

Другие формулы:

• тригонометрические функции углов;
• сумма тригонометрических функций;
• разность тригонометрических функций;
• произведение тригонометрических функций;
• тригонометрические функции суммы углов;
• тригонометрические функции разности углов;
• тригонометрические формулы приведения;
• тригонометрические функции кратных углов;
• тригонометрические функции двойного угла;
• тригонометрические функции половинного угла;
• тригонометрические функции угла, полученного многократным делением пи на два;
• выражение тригонометрических функций через другую;
• выражение тригонометрических функций через гиперболические;
• тригонометрические функции комплексной переменной;
• производные тригонометрических функций;
• дифференциалы тригонометрических функций;
• интегралы тригонометрических функций;
• графики тригонометрических функций.

Ссылки

• Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.183.
• Участник:Logic-samara