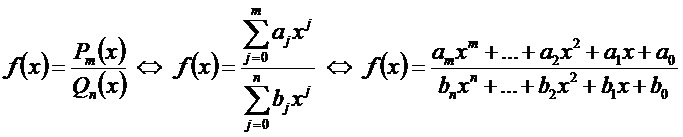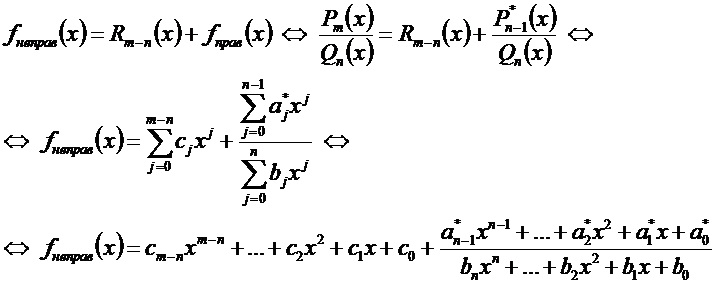Дробно-рациональная функция — различия между версиями
м |
м |
||
| Строка 3: | Строка 3: | ||
== Обозначения == | == Обозначения == | ||
Введём обозначения: | Введём обозначения: | ||
| + | |||
| + | '''f(x)''' — дробно-рациональная функция; | ||
| + | |||
| + | '''f<sub>прав</sub>(x)''' — правильная рациональная дробь; | ||
| + | |||
| + | '''f<sub>неправ</sub>(x)''' — неправильная рациональная дробь; | ||
'''P<sub>m</sub>(x)''' — многочлен степени '''m'''; | '''P<sub>m</sub>(x)''' — многочлен степени '''m'''; | ||
| Строка 14: | Строка 20: | ||
[[файл:ДФ01.JPG]] | [[файл:ДФ01.JPG]] | ||
== Определения == | == Определения == | ||
| − | '''Дробно-рациональная функция''' называется '''правильной''', если степень числителя меньше степени знаменателя, т.е. '''m<n'''. | + | '''Дробно-рациональная функция''' называется '''правильной рациональной дробью''', если степень числителя меньше степени знаменателя, т.е. '''m<n'''. |
| − | '''Дробно-рациональная функция''' называется '''неправильной''', если степень числителя не меньше степени знаменателя, т.е. '''m≥n'''. | + | '''Дробно-рациональная функция''' называется '''неправильной рациональной дробью''', если степень числителя не меньше степени знаменателя, т.е. '''m≥n'''. |
| − | == Свойства | + | == Свойства функции == |
[[файл:ДФ02.JPG]] | [[файл:ДФ02.JPG]] | ||
== [[Функции|Другие функции:]] == | == [[Функции|Другие функции:]] == | ||
Версия 19:51, 8 января 2021
Дробно-рациональная функция − это функция, равная отношению двух многочленов.
Содержание
Дробно-рациональные функции
Обозначения
Введём обозначения:
f(x) — дробно-рациональная функция;
fправ(x) — правильная рациональная дробь;
fнеправ(x) — неправильная рациональная дробь;
Pm(x) — многочлен степени m;
Qn(x) — многочлен степени n;
Pn-1(x) — многочлен степени n-1;
Rm-n(x) — многочлен степени m-n при m≥n.
Вид функции
Определения
Дробно-рациональная функция называется правильной рациональной дробью, если степень числителя меньше степени знаменателя, т.е. m<n.
Дробно-рациональная функция называется неправильной рациональной дробью, если степень числителя не меньше степени знаменателя, т.е. m≥n.