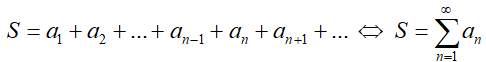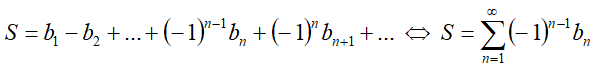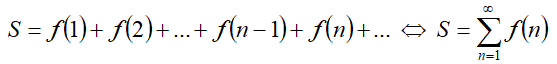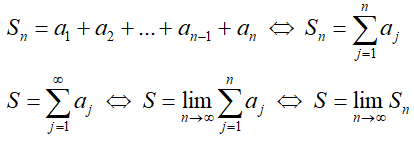Ряд — различия между версиями
| Строка 34: | Строка 34: | ||
'''[[Интегральный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии существования интеграла интегрируемой функции [[файл:РЯД035.png]]. | '''[[Интегральный признак Коши]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии существования интеграла интегрируемой функции [[файл:РЯД035.png]]. | ||
| − | '''[[Признак Раабе]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии | + | '''[[Признак Раабе]]''' используется для определения сходимости или расходимости ряда [[файл:РЯД00.png]], при условии [[файл:РЯД036.png]]. |
'''[[Признак Лейбница]]''' используется для определения сходимости знакопеременного ряда [[файл:РЯД001.png]], при условии [[файл:РЯД037.png]]. | '''[[Признак Лейбница]]''' используется для определения сходимости знакопеременного ряда [[файл:РЯД001.png]], при условии [[файл:РЯД037.png]]. | ||
Текущая версия на 14:20, 23 марта 2023
Ряд — это бесконечная последовательность слагаемых или бесконечная сумма членов последовательности.
Ряд
Формула
Слагаемые ряда an называются членами ряда.
Знакопеременными называются ряды, члены которых поочерёдно имеют то положительный, то отрицательный знаки. Общий вид знакопеременного ряда задаётся следующей формулой:
Если члены ряда — числа, то ряд называется числовым, если же они являются функциями (причём каждый член ряда определяется отдельной функцией fn(x)), то ряд называется функциональным. Члены числового ряда определяются одной функцией от числа f(n), например:
Сумма первых n членов называется частичной суммой Sn.
Сходимость ряда
Числовой ряд называется сходящимся, если существует конечный предел последовательности его частичных сумм — этот предел называется суммой ряда; в противном случае ряд называется расходящимся.
Признаки сходимости:
Необходимый признак используется для определения расходимости ряда 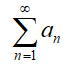 , при условии
, при условии 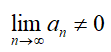 .
.
Признак сравнения используется или для определения сходимости меньшего (доминируемого) ряда 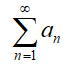 или для определения расходимости большего (доминирующего) ряда
или для определения расходимости большего (доминирующего) ряда 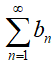 , при условии
, при условии ![]() .
.
Признак Даламбера используется для определения сходимости или расходимости ряда 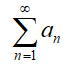 , при условии
, при условии 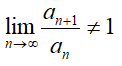 .
.
Радикальный признак Коши используется для определения сходимости или расходимости ряда 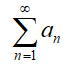 , при условии
, при условии 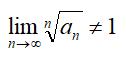 .
.
Интегральный признак Коши используется для определения сходимости или расходимости ряда 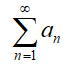 , при условии существования интеграла интегрируемой функции
, при условии существования интеграла интегрируемой функции 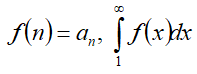 .
.
Признак Раабе используется для определения сходимости или расходимости ряда 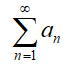 , при условии
, при условии 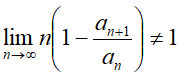 .
.
Признак Лейбница используется для определения сходимости знакопеременного ряда 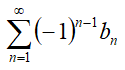 , при условии
, при условии ![]() .
.
Другие ряды:
Другие понятия:
Ссылки
- Кудрявцев В.А., Демидович Б.П. Краткий курс высшей математики. М.: «Наука», 1975.
- Участник:Logic-samara