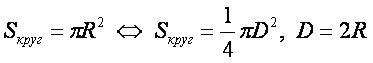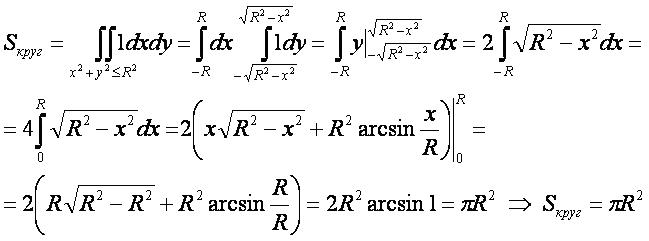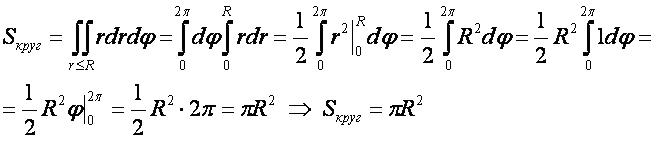Площадь круга — различия между версиями
Залт (обсуждение | вклад) (Отмена правки 107631 участника Iscorka (обсуждение):) |
Iscorka (обсуждение | вклад) м (Откат правок Залт (обсуждение) к версии Iscorka) |
||
| Строка 1: | Строка 1: | ||
[[файл:КРУ01.JPG|thumb|300|Круг]] | [[файл:КРУ01.JPG|thumb|300|Круг]] | ||
'''Площадь круга''' — это число, характеризующее [[Длина дуги окружности|круг]] в единицах измерения площади. | '''Площадь круга''' — это число, характеризующее [[Длина дуги окружности|круг]] в единицах измерения площади. | ||
| − | + | ||
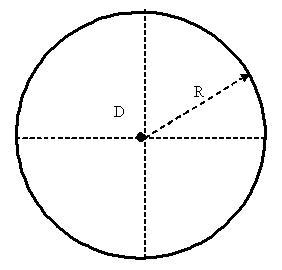
'''Круг''' — это геометрическое место точек, для которых расстояние от заданной точки (центра) не превышает постоянной величины (радиуса). | '''Круг''' — это геометрическое место точек, для которых расстояние от заданной точки (центра) не превышает постоянной величины (радиуса). | ||
== Обозначения == | == Обозначения == | ||
| Строка 7: | Строка 7: | ||
'''R''' — радиус; | '''R''' — радиус; | ||
| − | + | ||
'''D''' — диаметр; | '''D''' — диаметр; | ||
Версия 16:57, 23 января 2023
Площадь круга — это число, характеризующее круг в единицах измерения площади.
Круг — это геометрическое место точек, для которых расстояние от заданной точки (центра) не превышает постоянной величины (радиуса).
Содержание
Обозначения
Введём обозначения:
R — радиус;
D — диаметр;
Sкруг — площадь круга.
Формула
- Круг является фигурой постоянной ширины максимальной площади.
Вывод формулы:
1-ый способ
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется формула 3 интегралы функций с корнями.
2-ой способ
- Для вывода используется формула "площадь плоской фигуры" в полярных координатах.
Другие фигуры:
- плоская фигура;
- круг;
- сегмент круга;
- сектор круга;
- сегмент правильного многоугольника;
- сектор правильного многоугольника;
- серп;
- сегмент параболы;
- эллипс;
- сегмент эллипса;
- сектор эллипса;
- серп эллипса;
- сегмент гиперболы;
- арка синусоиды;
- арка косинусоиды;
- фигура, ограниченная тангенсоидой и осью абсцисс;
- фигура, ограниченная котангенсоидой и осью абсцисс;
- арка циклоиды;
- сектор кардиоиды;
- фигура, ограниченная цепной линией и осью абсцисс;
- фигура, ограниченная трактрисой и осью абсцисс;
- сектор лемнискаты Бернулли.