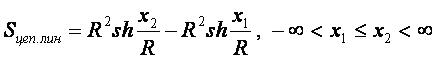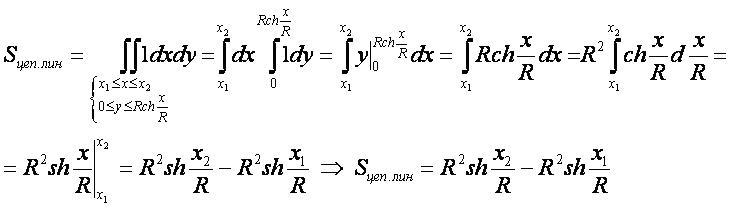Площадь, ограниченная цепной линией и осью абсцисс

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

Цепная линия

Площадь, ограниченная цепной линией и осью абсцисс, — это число, характеризующее область под цепной линией в пределах -∞<x₁≤x₂<∞ в единицах измерения площади.

Цепная линия (висящая цепь) — это линия, образуемая гибкой тяжёлой нерастяжимой нитью (цепью), подвешенной в двух точках. График цепной линии имеет вид графика гиперболического косинуса.

Рассмотрим дуги цепной линии, с вершиной в точке (0,R).

Обозначения

Введём обозначения:

x₁ — абсцисса (меньшая) первой (левой) точки;

x₂ — абсцисса (большая) второй (правой) точки;

M=(x,y) — точка цепной линии;

M₀=(0,R) — вершина цепной линии;

y=Rch(x/R) — уравнение цепной линии;

S_{цеп.лин} — площадь, ограниченная цепной линией и осью абсцисс при -∞<x₁≤x₂<∞.

Формула

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

• Площадь, ограниченная дугой цепной линии M₀M и осью абсцисс, равна S_x=R²sh(x/R).

Вывод формулы:

Ошибка создания миниатюры: Не удаётся сохранить эскиз по месту назначения

• Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.

Другие фигуры:

• плоская фигура;
• круг;
• сегмент круга;
• сектор круга;
• сегмент правильного многоугольника;
• сектор правильного многоугольника;
• серп;
• сегмент параболы;
• эллипс;
• сегмент эллипса;
• сектор эллипса;
• серп эллипса;
• сегмент гиперболы;
• арка синусоиды;
• арка косинусоиды;
• фигура, ограниченная тангенсоидой и осью абсцисс;
• фигура, ограниченная котангенсоидой и осью абсцисс;
• арка циклоиды;
• сектор кардиоиды;
• фигура, ограниченная цепной линией и осью абсцисс;
• фигура, ограниченная трактрисой и осью абсцисс;
• сектор лемнискаты Бернулли.

Ссылки

• Участник:Logic-samara