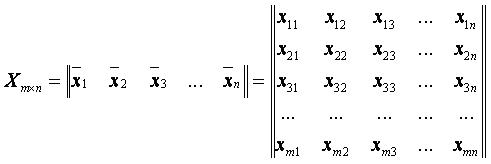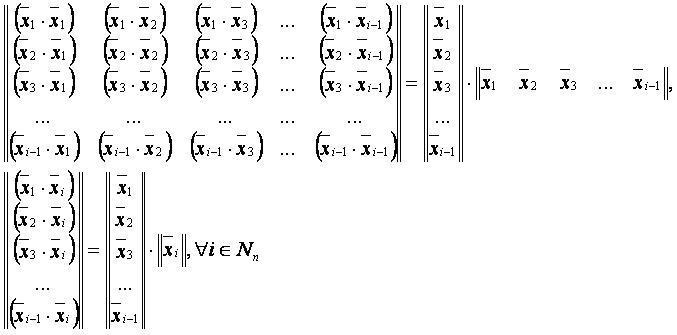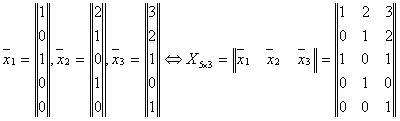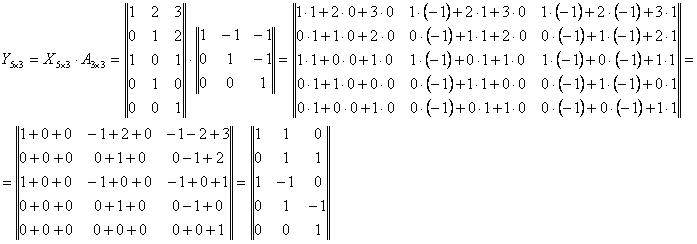Метод Грама-Шмидта — различия между версиями
м |
м |
||
| Строка 60: | Строка 60: | ||
= Ссылки = | = Ссылки = | ||
*Беллман Р. Введение в теорию матриц. М.: Наука, 1976, стр. 65. | *Беллман Р. Введение в теорию матриц. М.: Наука, 1976, стр. 65. | ||
| − | |||
[[Категория:Математика]][[Категория:Векторы]][[Категория:Численные методы]][[Категория:Алгоритмы]] | [[Категория:Математика]][[Категория:Векторы]][[Категория:Численные методы]][[Категория:Алгоритмы]] | ||
Версия 15:19, 23 октября 2024
Метод Грама-Шмидта — это способ ортогонализации системы линейно-независимых векторов.
Содержание
Ортогонализация
Описание метода
Суть метода Грама-Шмидта состоит во взятии первого ортогонального вектора равным первому исходному вектору и построении каждого нового ортогонального вектора равным текущему исходному вектору, скорректированному на величины проекций текущего вектора на предыдущие ортогональные векторы.
Исходная система линейно-независимых векторов имеет вид:
Алгоритм решения
Основные формулы в векторном виде.
Основные формулы в координатном виде.
Система ортогональных векторов принимает вид:
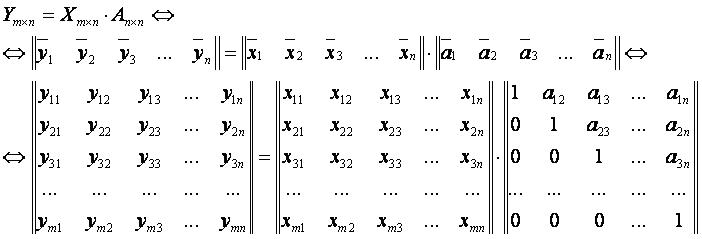
Процесс ортогонализации можно выразить в матричном виде.
Для этого проведём подготовительные расчёты.
где верны равенства:
Процесс ортогонализации превращается в обычное умножение матриц.
Пример решения
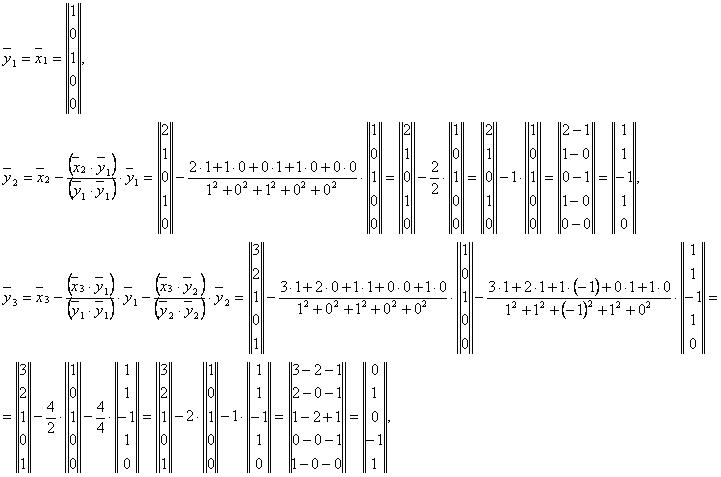
Дана система векторов:
Ортогонализируем систему векторов методом Грама-Шмидта.
В результате получаем ортогональную систему векторов:
Для решения с помощью матриц проведём подготовительные расчёты.
Ортогонализируем систему векторов умножением матриц.
Другие операции:
- нахождение длины вектора;
- умножение вектора на число;
- возведение в квадрат координат вектора;
- извлечение корня из координат вектора;
- сложение векторов;
- вычитание векторов;
- умножение координат векторов;
- деление координат векторов;
- скалярное произведение;
- векторное произведение;
- смешанное произведение;
- двойное векторное произведение;
- нахождение угла между векторами;
- ортогонализация векторов.
Численные методы:
Другие разделы
Ссылки
- Беллман Р. Введение в теорию матриц. М.: Наука, 1976, стр. 65.