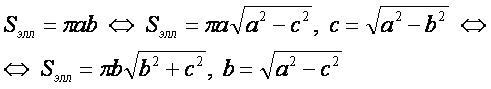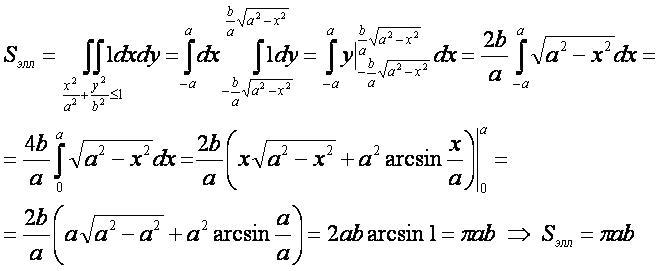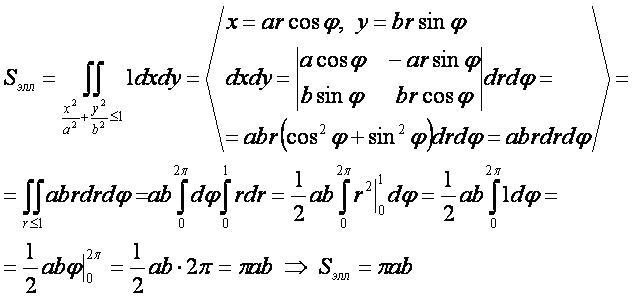Площадь эллипса — различия между версиями
(начало) |
м |
||
| Строка 4: | Строка 4: | ||
'''Эллипс''' — это геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов) есть величина постоянная (большая ось эллипса). | '''Эллипс''' — это геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов) есть величина постоянная (большая ось эллипса). | ||
== Обозначения == | == Обозначения == | ||
| − | |||
| − | |||
'''a''' — большая полуось; | '''a''' — большая полуось; | ||
| Строка 37: | Строка 35: | ||
== Ссылки == | == Ссылки == | ||
*Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.207. | *Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.207. | ||
| − | + | [[Категория:Математика]][[Категория:Формулы]] | |
| − | [[Категория: | ||
Текущая версия на 16:17, 18 февраля 2025
Площадь эллипса — это число, характеризующее эллипс в единицах измерения площади.
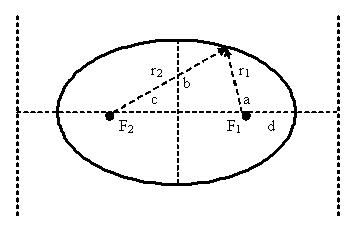
Эллипс — это геометрическое место точек, для которых сумма расстояний от двух заданных точек (фокусов) есть величина постоянная (большая ось эллипса).
Содержание
Обозначения
a — большая полуось;
b — малая полуось;
c — расстояние от центра до фокуса;
d — расстояние от центра до директрисы;
r1 — расстояние от правого фокуса до точки эллипса;
r2 — расстояние от левого фокуса до точки эллипса;
Sэлл — площадь эллипса.
Формула
Вывод формулы:
1-ый способ
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется формула 3 интегралы функций с корнями.
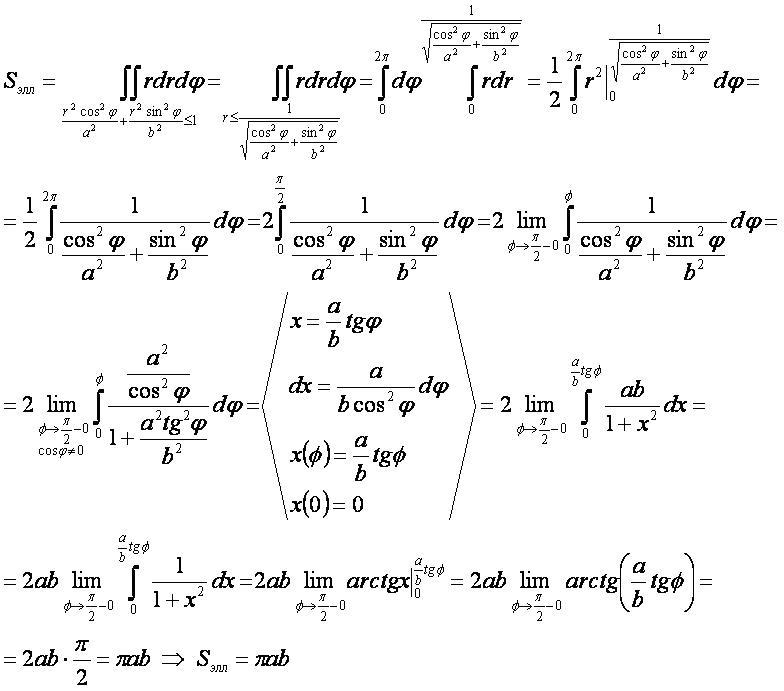
2-ой способ
- Для вывода используется формула "площадь плоской фигуры" в полярных координатах.
3-ий способ
- Для вывода используется формула "площадь плоской фигуры" в прямоугольных координатах.
- Для нахождения интеграла используется метод замены переменных и переход к полярным координатам.
Другие фигуры:
- плоская фигура;
- круг;
- сегмент круга;
- сектор круга;
- сегмент правильного многоугольника;
- сектор правильного многоугольника;
- серп;
- сегмент параболы;
- эллипс;
- сегмент эллипса;
- сектор эллипса;
- серп эллипса;
- сегмент гиперболы;
- арка синусоиды;
- арка косинусоиды;
- фигура, ограниченная тангенсоидой и осью абсцисс;
- фигура, ограниченная котангенсоидой и осью абсцисс;
- арка циклоиды;
- сектор кардиоиды;
- фигура, ограниченная цепной линией и осью абсцисс;
- фигура, ограниченная трактрисой и осью абсцисс;
- сектор лемнискаты Бернулли.
Ссылки
- Бронштейн М.Н., Семендяев К.А., Справочник по математике. М., 1956, стр.207.