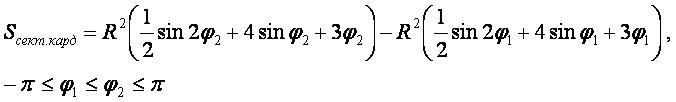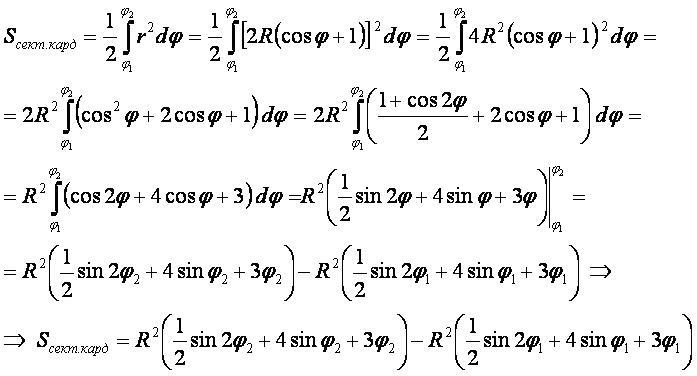Площадь сектора кардиоиды
Площадь сектора кардиоиды — это число, характеризующее сектор кардиоиды в единицах измерения площади.
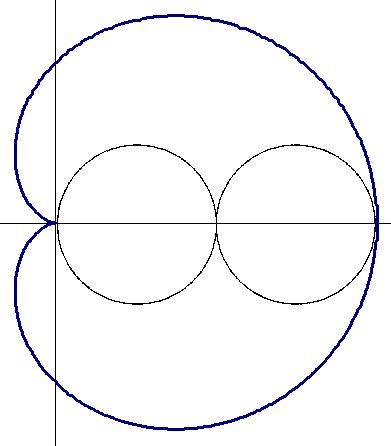
Сектор кардиоиды — это часть кардиоиды, отсекаемая двумя прямыми (радиусами), проходящими через начало координат оси симметрии.
Рассмотрим сектора кардиоиды при -π≤φ≤π.
Обозначения
Введём обозначения:
x1 — абсцисса первой точки;
y1 — ордината первой точки;
φ1 — угол (меньший) первой точки;
x2 — абсцисса второй точки;
y2 — ордината второй точки;
φ2 — угол (больший) второй точки;
R — радиус производящей окружности;
φ — независимая переменная;
r=2R(1+cosφ) — уравнение кардиоиды в полярных координатах;
t — параметрическая переменная;
x=2Rcost(1+cost) — параметрическое уравнение абсциссы кардиоиды;
y=2Rsint(1+cost) — параметрическое уравнение ординаты кардиоиды;
Sсект.кард — площадь сектора кардиоиды.
Формула
- Площадь полной (от -π до π) кардиоиды равна площади шести производящих кругов, Sкард=6πR2.
Вывод формулы
- Для вывода используется формула "площадь плоской фигуры" в полярных координатах.
Другие фигуры:
- плоская фигура;
- круг;
- сегмент круга;
- сектор круга;
- сегмент правильного многоугольника;
- сектор правильного многоугольника;
- серп;
- сегмент параболы;
- эллипс;
- сегмент эллипса;
- сектор эллипса;
- серп эллипса;
- сегмент гиперболы;
- арка синусоиды;
- арка косинусоиды;
- фигура, ограниченная тангенсоидой и осью абсцисс;
- фигура, ограниченная котангенсоидой и осью абсцисс;
- арка циклоиды;
- сектор кардиоиды;
- фигура, ограниченная цепной линией и осью абсцисс;
- фигура, ограниченная трактрисой и осью абсцисс;
- сектор лемнискаты Бернулли.